Question

Discuss the properties of scalar and vector products.

Answer 1

Properties of the scalar product of two vectors are:

(1) The product quantity `vecA` . `vecB` is always a scalar. It is positive if the angle between the vectors is acute (i.e., < 90°) and negative if the angle between them is obtuse (i.e. 90°< 0 < 180°).

(2) The scalar product is commutative, i.e. `vecA vecB  ± vecB . vecA`

(3) The vectors obey distributive law i.e. `vecA(vecB + vecC) = vecA . vecB + vecA . vecC`

(4) The angle between the vectors θ = `cos^-1[(vecA.vecB)/(AB)]`

(5) The scalar product of two vectors will be maximum when cos θ = 1, i.e. θ = 0°, i.e., when the vectors are parallel;

`(vecA . vecB)_"max" = AB`

(6) The scalar product of two vectors will be minimum, when cos θ = -1, i.e. θ = 180°.

`(vecA . vecB)_"min" = -AB` when the vectors are anti-parallel.

(7) If two vectors `vecA` and `vecB` are perpendicular to each other then their scalar product `vecA` . `vecB` = 0, because cos 90° 0. Then the vectors `vecA` and `vecB` are said to be mutually orthogonal.

(8) The scalar product of a vector with itself is termed as self-dot product and is given by `(vecA)^2 = vecA . vecA = A A cos 0 = A^2`. Here angle 0 = 0°.

The magnitude or norm of vector `vecA` is `|vecA| = A = sqrt(vecA . vecA.)`

(9) In case of a unit vector `hatn`
`hatn . hatn` = 1 × 1 × cos 0 = 1. For example, `hati - hatj = hatj . hatj = hatk . hatk = 1.`

(10) In the case of orthogonal unit vectors, `hati, hatj` and `hatk`, `hati . hatj = hatj . hatk = hatk . hat i = 1.1` cos 90° = 0

(11) In terms of components the scalar product of `vecA` and `vecB` can be written as `vecA . vecB = (A_xhati + A_yhatj + A_zhatk) . (B_xhati + B_yhatj + B_Zhatk)`

= A_xB_x + A_yB_y+ A_zB_z, with all other terms zero.

The magnitude of vector `|vecA|` is given by 

`|vecA| = A = sqrt(A_x^2 + A_y^2 + A_z^2)`

Properties of the vector product of two vectors are:

(1) The vector product of any two vectors is always another vector whose direction is perpendicular to the plane containing these two vectors, i.e., orthogonal to both the vectors `vecA` and `vecB`, even though the vectors `vecA` and `vecB` may or may not be mutually orthogonal.

(2) The vector product of two vectors is not commutative, i.e., `vecA xx vecB ≠ vecB xx vecA`. But,`vecA xx vecB = -vecB xx vecA.`

Here it is worthwhile to note that `|vecA xx vecB| = |vecB xx vecA|` = AB sin 0 i.e., in the case of the product vectors `vecB = -vecB  "and"  vecB xx vecA,` the magnitudes are equal but directions are opposite to each other.

(3) The vector product of two vectors will have maximum magnitude when sin 0 = 1, i.e., 0 = 90° i.e. when the vectors `vecA` and `vecB` are orthogonal to each other.

`(vecA xx vecB)_"maz" = AB  hatn = AB  hatn`

(4) The vector product of two non-zero vectors will be minimum when sin θ = 0, i.e θ = 0° or 180° `(vecA xx vecB)_"min" = 0`

i. e., the vector product of two non – zero vectors vanishes, if the vectors are either parallel or anti-parallel.

(5) The self–cross product, i.e., a product of a vector with itself is the null vector `vecA xx vecA` = AA sin 0° `hatn` = `vec0` In physics, the null vector 0 is simply denoted as zero.

(6) The self–vector products of unit vectors are thus zero. `hati xx hati = hatj xx hatj = hatk xx hatk = 0`

(7) In the case of orthogonal unit vectors, `hati, hatj, hatk,` in accordance with the right-hand screw rule:
`hati xx hatj = hatk, hatj xx hatk = hati  "and"  hatk xx hati = hatj`

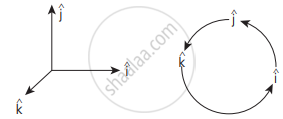
Also, since the cross product is not commutative, `hatj xx hati = -hatk. hatk xx hatj = -hati` and `hati xx hatk = hatj`

(8) In terms of components, the vector product of two vectors `vecA` and `vecB` is - 

`vecA xx vecB = |(hati     hatj     hat k), (A_x  A_y  A_z), (B_x  B_y  B_z)|`

= `hati(A_yB_z - A_zB_y) + hatj(A_zB_x - A_xB_z) + hatk(A_xB_y - A_yB_x)`

Note that in the `hatj^"th"` component the order of multiplication is different than `hati^"th"` and `hatk^"th"` components.

(9) If two vectors `vecA` and `vecB` form adjacent sides in a parallelogram, then the magnitude of `|vecA xx vecB|` will give the area of the parallelogram as represented graphically in figure.

`|vecA xx vecB| = |vecA| |vecB| sintheta`

 

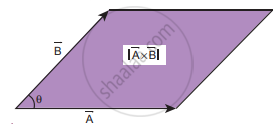
Area of parallelogram

(10) Since we can divide a parallelogram into two equal triangles as shown in the figure, the area of a triangle with `vecA` and `vecB` as sides is `1/2 |vecA xx vecB|`. This is shown in the Figure. A number of quantities used in Physics are defined through vector products. Particularly physical quantities representing rotational effects like torque, angular momentum, are defined through vector products.

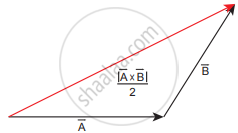
Area of triangle