Advertisements
Advertisements
प्रश्न
Draw a circle of radius 4.2 cm, take any point M on it. Draw tangent to the circle from point M
उत्तर
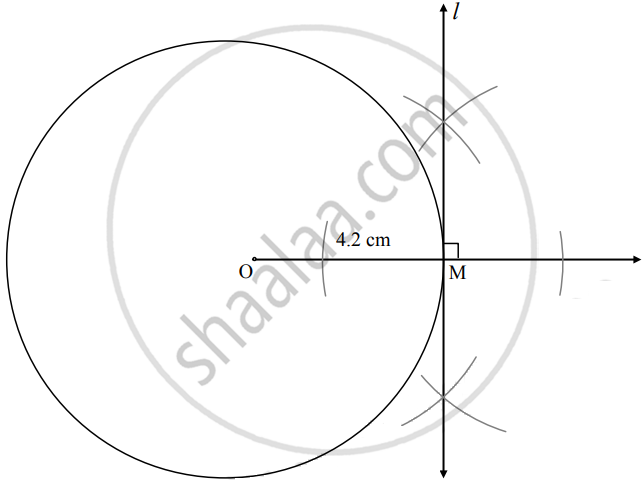
Steps of construction:
- With center O, draw a circle of radius 4.2 cm.
- Take any point M on the circle and draw ray OM.
- Draw line l ⊥ ray OM at point M.
Line l is the required tangent to the circle at point M.
APPEARS IN
संबंधित प्रश्न
Construct a tangent to a circle with centre P and radius 3.2 cm at any point M on it.
Select the correct alternative for the following question.
The maximum number of tangents that can be drawn to a circle from a point out side it is .............. .
Select the correct alternative for the following question.
(3) If ∆ABC ~ ∆PQR and `(AB)/(PQ) = 7/5`, then ...............
Draw a circle with centre O and radius 3.5 cm. Take point P at a distance 5.7 cm from the centre. Draw tangents to the circle from point P.
Draw any circle. Take any point A on it and construct tangent at A without using the centre of the circle.
Choose the correct alternative:
The tangents drawn at the end of a diameter of a circle are ______
Choose the correct alternative:
Which theorem is used while constructing a tangent to the circle by using center of a circle?
Draw a circle of radius 3 cm and draw a tangent to the circle from point P on the circle
| Draw a circle with center O and radius 3 cm |
| ↓ |
| Take any point P on the circle |
| ↓ |
| Draw ray OP |
| ↓ |
| Draw perpendicular to ray OP from point P |
Complete the following activity to draw tangents to the circle.
- Draw a circle with radius 3.3 cm and center O. Draw chord PQ of length 6.6 cm. Draw ray OP and ray OQ.
- Draw a line perpendicular to the ray OP from P.
- Draw a line perpendicular to the ray OQ from Q.
Do the following activity to draw tangents to the circle without using the center of the circle.
- Draw a circle with radius 3.5 cm and take any point C on it.
- Draw chord CB and an inscribed angle CAB.
- With the center A and any convenient radius, draw an arc intersecting the sides of angle BAC in points M and N.
- Using the same radius, draw an arc intersecting the chord CB at point R.
- Taking the radius equal to d(MN) and center R, draw an arc intersecting the arc drawn in the previous step. Let D be the point of intersection of these arcs. Draw line CD. Line CD is the required tangent to the circle.
Draw a circle with center O and radius 3.4. Draw a chord MN of length 5.7 cm in a circle. Draw tangents to the circle from point M and N
Draw a circle with center C and radius 3.2 cm. Draw a tangent to the circle from point P at a distance of 7.5 cm from the center of the circle
Draw a circle of radius 4.2 cm. Draw arc PQ measuring 120°. Draw a tangent to the circle from point P and point Q
AB = 6 cm, ∠BAQ = 50°. Draw a circle passing through A and B so that AQ is the tangent to the circle
Draw a circle with radius 3 cm. Construct a square such that each of its side will touch the circle from outside
Take point P and Q and draw a circle passing through them. Draw a tangent AB to the circle without using the centre of the circle.
Draw a circle with center O and radius 2.8 cm. Take point P in the exterior of a circle such that tangents PA and PB drawn from point P make an angle ∠APB of measure 70°
Draw a circle of radius 4 cm. Draw a point 8 cm away from its centre and construct a pair of tangents.
