Advertisements
Advertisements
प्रश्न
Draw any line segment, say `overline"AB"`. Take any point C lying in between A and B. Measure the lengths of AB, BC, and AC. Is AB = AC + CB?
[Note: If A, B, and C are any three points on a line such that AC + CB = AB, then we can be sure that C lies between A and B.]
उत्तर
It is given that point C is lying somewhere in between A and B. Therefore, all these points are lying on the same line segment `overline"AB"`. Hence, for every situation at which point C is lying in between A and B, it may be said that AB = AC + CB.
For example,
`overline"AB"` is a line segment of 6 cm and C is a point between A and B, such that it is 2 cm away from point B. We can find that the measure of line segment `overline"AC"` comes to 4 cm.
Hence, relation AB = AC + CB is verified.
APPEARS IN
संबंधित प्रश्न
Measure the following line segments.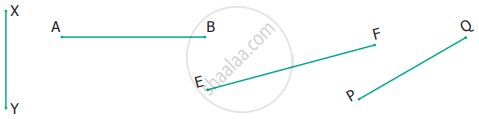
From the given figure, name the
(i) parallel lines
(ii) intersecting lines
(iii) points of intersection.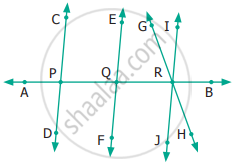
Find the type of lines marked in thick lines
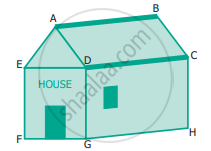
Find the type of lines marked in thick lines
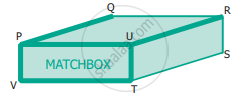
Find the type of lines marked in thick lines
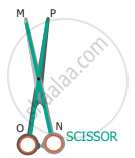
Find the parallel and intersecting line segments in the picture given below.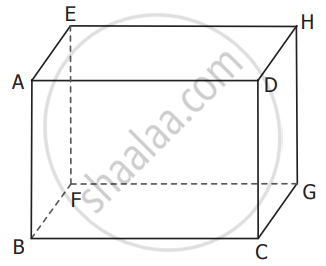
What is the disadvantage of comparing line segments by mere observation?
Why is it better to use a divider than a ruler, while measuring the length of a line segment?
If A, B, and C are three points on a line such that AB = 5 cm, BC = 3 cm, and AC = 8 cm, which one of them lies between the other two?
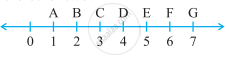
Verify, whether D is the midpoint of `overline"AG"`.