Question

Earth has mass M₁ and radius R₁. Moon has mass M₂ and radius R₂. Distance between their centre is r. A body of mass M is placed on the line joining them at a distance `"r"/3` from centre of the earth. To project the mass M to escape to infinity, the minimum speed required is ______.

विकल्प

• `["3G"/"r" ("M"_1 + "M"_2/2)]^(1/2)`

• `["6G"/"r" ("M"_1 + "M"_2/2)]^(1/2)`

• `["6G"/"r" ("M"_1 - "M"_2/2)]^(1/2)`

• `["3G"/"r" ("M"_1 - "M"_2/2)]^(1/2)`

Answer 1

Earth has mass M₁ and radius R₁. Moon has mass M₂ and radius R₂. Distance between their centre is r. A body of mass M is placed on the line joining them at a distance `"r"/3` from centre of the earth. To project the mass M to escape to infinity, the minimum speed required is `underline(["6G"/"r" ("M"_1 + "M"_2/2)]^(1/2))`.

Explanation:

The given situation can be drawn as

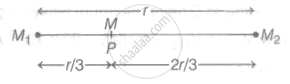
The gravitational potential at P is

`"V"_"P" = - ("GM"_1/("r"/3) + "GM"_2/("2r"/3))`

`= (- 3"G"(2"M"_1 + "M"_2))/"2r"`

The work done to escape the mass M to infinity is

W = `"M"("V"_∞ - "V"_"P") = (3"GM" (2"M"_1 + "M"_2))/"2r"`

As, work done is equal to kinetic energy of mass M.

`=> 1/2 "Mv"_e^2 = (3"GM" (2"M"_1 + "M"_2))/"2r"`

`"v"_e = ["3G"/"r" (2"M"_1 + "M"_2)]^(1//2)`

or `"v"_e = ["6G"/"r" ("M"_1 + "M"_2/2)]^(1//2)`