Advertisements
Advertisements
प्रश्न
एक चतुर्भुज ABCD की भुजाओं के मध्य-बिंदुओं को, एक ही क्रम में, मिलाने पर प्राप्त आकृति केवल एक वर्ग है, यदि ______।
विकल्प
ABCD एक समचतुर्भुज है
ABCD के विकर्ण बराबर हैं
ABCD के विकर्ण बराबर हैं और परस्पर लंब हैं
ABCD के विकर्ण परस्पर लंब हैं
उत्तर
एक चतुर्भुज ABCD की भुजाओं के मध्य-बिंदुओं को, एक ही क्रम में, मिलाने पर प्राप्त आकृति केवल एक वर्ग है, यदि ABCD के विकर्ण बराबर हैं और परस्पर लंब हैं।
स्पष्टीकरण -
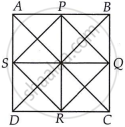
दिया गया है, ABCD एक चतुर्भुज है और P, Q, R और S क्रमश : भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं।
फिर, PQRS एक वर्ग है।
∴ PQ = QR = RS = PS ...(i)
और PR = SQ
लेकिन PR = BC और SQ = AB
∴ AB = BC
इस प्रकार, चतुर्भुज ABCD की सभी भुजाएँ बराबर हैं।
अतः, चतुर्भुज ABCD या तो एक वर्ग या एक समचतुर्भुज है।
अब, ∆ADB में, मध्य-बिंदु प्रमेय का प्रयोग करें।
SP || DB
और SP = `1/2` DB ...(ii)
इसी प्रकार △ABC में ...(मध्य-बिंदु प्रमेय द्वारा)
PQ || AC और PQ = `1/2` AC ...(iii)
समीकरण (i) से,
PS = PQ
⇒ `1/2` DB = `1/2` AC ...[समीकरण (ii) और (iii) से]
⇒ DB = AC
इस प्रकार, ABCD के विकर्ण बराबर हैं और इसलिए चतुर्भुज ABCD एक वर्ग है न कि समचतुर्भुज। इसलिए, चतुर्भुज के विकर्ण भी लंबवत होते हैं।
APPEARS IN
संबंधित प्रश्न
चतुर्भुज PQRS, की भुजाओं के मध्य-बिंदुओं को, एक ही क्रम में, मिलाने पर बना चतुर्भुज एक आयत होता है, यदि ______।
0° का कोण एक न्यूनकोण है।
9 बजे घड़ी की घंटे तथा मिनट की सूइयों के बीच में बने कोणों के माप हैं:
यदि एक साइकिल के पहिए में 48 तीलियाँ (spokes) हों, तो दो क्रमागत तीलियों के बीच का कोण है
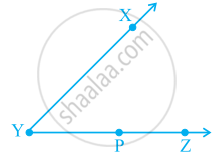
आकृति में, ∠ XYZ को निम्नलिखित में से किस रूप में नहीं लिखा जा सकता है?
आकृति में, अधिक कोणों की संख्या है-

आकृति में
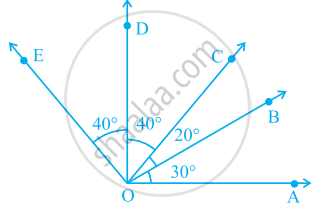
∠AOE एक ____ कोण है।
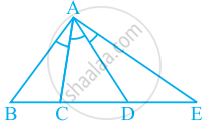
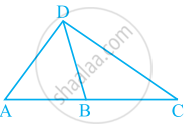
आकृति के भाग से क्या निष्कर्ष निकाला जा सकता है, यदि DB कोण ADC का समद्धिभाजक है?
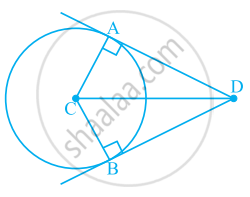
आकृति के भाग से क्या निष्कर्ष निकाला जा सकता है, यदि DC कोण ADB का समद्विभाजक है, CA ⊥ DA और CB ⊥ DB है?
किसी कोण को तीन बराबर भागों में बाँट देने पर उसे समनत्रिभाजित हुआ कहा जाता है। यदि आकृति में, ∠BAC = ∠CAD = ∠DAE है, तो ∠BAE के लिए कितने समत्रिभाजक हैं?