Advertisements
Advertisements
प्रश्न
एका वर्तुळाची त्रिज्या 10 सेमी असून त्याच्या एका जीवेचे केंद्रापासूनचे अंतर 6 सेमी आहे, तर त्या जीवेची लांबी किती?
विकल्प
16 सेमी
8 सेमी
12 सेमी
32 सेमी
उत्तर
16 सेमी
स्पष्टीकरण:
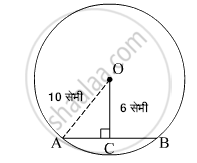
समजा, जीवा AB आहे.
O हा वर्तुळाचा केंद्रबिंदु आहे आणि OC हा वर्तुळाच्या केंद्रापासून जीवा AB वर काढलेला लंब आहे.
वर्तुळकेंद्रातून जीवेवर टाकलेला लंब जीवेला दुभागतो.
AC = CB
OA = 10 सेमी
ΔOAC मध्ये,
OC2 + AC2 = OA2
⇒ 62 + AC2 = 102
⇒ 36 + AC2 = 100
⇒ AC2 = 64
⇒ AC = 8 सेमी
AC = CB = 8 सेमी
AB = AC + CB
= 8 + 8
= 16 सेमी
APPEARS IN
संबंधित प्रश्न
वर्तुळकेंद्र O पासून जीवा AB चे अंतर 8 सेमी आहे. जीवा AB ची लांबी 12 सेमी आहे, तर वर्तुळाचा व्यास काढा.
एका वर्तुळाचा व्यास 26 सेमी असून जीवेची लांबी 24 सेमी आहे, तर त्या जीवेचे केंद्रापासूनचे अंतर काढा.
वर्तुळाच्या केंद्रापासून जीवेचे अंतर 30 सेमी असून वर्तुळाची त्रिज्या 34 सेमी आहे, तर जीवेची लांबी काढा.
O केंद्र असलेल्या वर्तुळाची त्रिज्या 41 सेमी आहे. वर्तुळाची जीवा PQ ची लांबी 80 सेमी आहे, तर जीवा PQ चे केंद्रापासूनचे अंतर काढा.
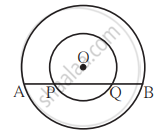
खालील आकृती मध्ये केंद्र O असलेली दोन वर्तुळे आहेत. मोठ्या वर्तुळाची AB ही जीवा लहान वर्तुळाला बिंदू P व Q मध्ये छेदते. तर सिद्ध करा: AP = BQ
सिद्ध करा की, वर्तुळाचा व्यास जर वर्तुळाच्या दोन जीवांना दुभागत असेल तर त्या जीवा परस्परांना समांतर असतात.
2.9 सेमी त्रिज्या असणाऱ्या वर्तुळात जास्तीत जास्त किती लांबीची जीवा असू शकते?
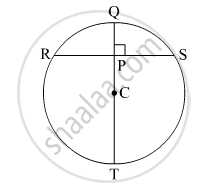
खालील आकृती मध्ये C हे वर्तुळाचे केंद्र आहे. रेख QT हा व्यास आहे. CT = 13, CP = 5 असेल तर जीवा RS काढा.
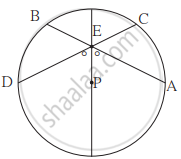
खालील आकृती मध्ये P हे वर्तुळाचे केंद्र आहे. जीवा AB आणि जीवा CD व्यासावर बिंदू E मध्ये छेदतात. जर ∠AEP ≅ ∠DEP तर सिद्ध करा, की AB = CD.
खालील आकृती मध्ये O केंद्र असलेल्या वर्तुळाचा CD हा व्यास व AB ही जीवा आहे. व्यास CD हा जीवा AB ला E बिंदूपाशी लंब आहे, तर दाखवा की ΔABC हा समद्विभुज त्रिकोण आहे.

