Advertisements
Advertisements
प्रश्न
Explain briefly seven types of unit cells.
Advertisements
उत्तर
Seven types of unit cells:
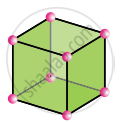
Cubic
a = b = c
α = β = γ = 90°
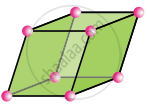
Rhombohedral
a = b = c
α = β = γ ≠ 90°
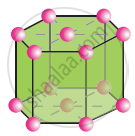
Hexagonal
a = b ≠ c
α = β = 90°, γ = 120°
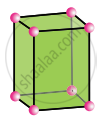
Tetragonal
a = b ≠ c
α = β = γ = 90°
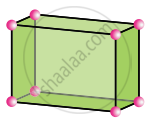
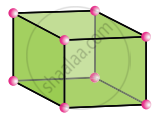
Orthorhombic
a ≠ b ≠ c
α = β = γ = 90°
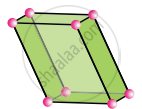
Monoclinic
a ≠ b ≠ c
α = γ = 90°, β ≠ 90°
Triclinic
a ≠ b ≠ c
α ≠ β ≠ γ ≠ 90°
- Cubic – NaCl
- Rhombohedral – Cinnabar Cubic
- Hexagonal – ZnO
- Tetragonal – TiO2
- Orthorhombic – BaSO4
- Monoclinic – PbCrO4
- Triclinic – H3BO3
They differ in the arrangements of their crystallographic axes and angles.
Corresponding to the above seven, Bravis defined 14 possible crystal systems as shown in the figure.
APPEARS IN
संबंधित प्रश्न
The radius of an atom is 300 pm, if it crystallizes in a face centered cubic lattice, the length of the edge of the unit cell is ____________.
If ‘a’ stands for the edge length of the cubic system; sc, bcc, and fcc. Then the ratio of radii of spheres in these systems will be respectively.
If ‘a’ is the length of the side of the cube, the distance between the body-centered atom and one corner atom in the cube will be ______.
Calculate the number of atoms in a fcc unit cell.
What is meant by the term “coordination number”?
An element has bcc structure with a cell edge of 288 pm. The density of the element is 7.2 g cm−3. How many atoms are present in 208 g of the element?
Aluminium crystallizes in a cubic close packed structure. Its metallic radius is 125 pm. calculate the edge length of the unit cell.
KF crystallizes in fcc structure like sodium chloride. calculate the distance between K+ and F− in KF.
(Given: density of KF is 2.48 g cm−3)
An atom crystallizes in fcc crystal lattice and has a density of 10 g cm−3 with unit cell edge length of 100 pm. calculate the number of atoms present in 1 g of crystal.
Sodium metal crystallizes in bcc structure with the edge length of the unit cell 4.3 × 10−8 cm. calculate the radius of a sodium atom.
