Advertisements
Advertisements
प्रश्न
Explain in detail the effect of a dielectric placed in a parallel plate capacitor.
उत्तर
- When the capacitor is disconnected from the battery:
Consider a capacitor with two parallel plates each of cross-sectional area A and are separated by a distance d. The capacitor is charged by a battery of voltage V0 and the charge stored is Q0. The capacitance of the capacitor without the dielectric is
`"C"_0 = "Q"_0/"V"_0` .....(1)
The battery is then disconnected from the capacitor and the dielectric is inserted between the plates. The introduction of dielectric between the plates will decrease the electric field. Experimentally it is found that the modified electric field is given by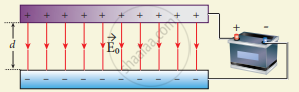
(a) Capacitor is charged with a battery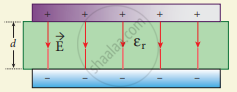
(b) Dielectric is inserted after the battery is disconnected
E = `"E"_0/ε_"r"` .....(2)
Here E0 is the electric field inside the capacitors when there is no dielectric and εr is the relative permeability of the dielectric or simply known as the dielectric constant. Since εr > 1, the electric field E < E0. As a result, the electrostatic potential difference between the plates (V = Ed) is also reduced. But at the same time, the charge Q0 will remain constant once the battery is disconnected. Hence the new potential difference is
V = Ed = `"E"_0/ε_"r" "d" = "V"_0/ε_"r"` ....(3)
We know that capacitance is inversely proportional to the potential difference. Therefore as V decreases, C increases. Thus new capacitance in the presence of a dielectric is
C = `"Q"_0/"V" = ε_"r" "Q"_0/"V"_0 = ε_"r" "C"_0` .....(4)
Since εr > 1, we have C > C0. Thus insertion of the dielectric constant εr increases the capacitance. Using equation,
C = `(ε_0"A")/"d"`
C = `(ε_"r"ε_0"A")/"d" = (ε"A")/"d"`......(5)
where ε = εrε0 is the permittivity of the dielectric medium. The energy stored in the capacitor before the insertion of a dielectric is given by U0 = `1/2 "Q"_0^2/"C"_0` .....(6)
After the dielectric is inserted, the charge Q0 remains constant but the capacitance is increased. As a result, the stored energy is decreased.
U = `1/2 "Q"_0^2/(2"C") = 1/2 "Q"_0^2/(2 ε_"r""C"_0) = "U"_0/ε_"r"`
Since εr> 1 we get U < U0. There is a decrease in energy because, when the dielectric is inserted, the capacitor spends some energy in pulling the dielectric inside.
- When the battery remains connected to the capacitor:
Let us now consider what happens when the battery of voltage V0 remains connected to the capacitor when the dielectric is inserted into the capacitor.
The potential difference V0 across the plates remains constant. But it is found experimentally (first shown by Faraday) that when dielectric is inserted, the charge stored in the capacitor is increased by a factor εr.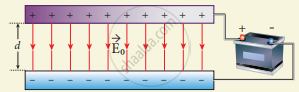
(a) Capacitor is charged through a battery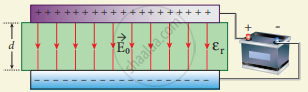
(b) Dielectric is inserted when the battery is connected.
Q = εrQ0 ….. (1)
Due to this increased charge, the capacitance is also increased. The new capacitance is
C = `"Q"_0/"V" = ε_"r" "Q"_0/"V"_0 = ε_"r" "C"_0` ....(2)
However the reason for the increase in capacitance in this case when the battery remains connected is different from the case when the battery is disconnected before introducing the dielectric.
Now, C0 = `(ε_0"A")/"d"` and, C = `(ε"A")/"d"` .....(3)
`"U"_0 = 1/2 "C"_0 "V"_0^2` ....(4)
Note that here we have not used the expression
`"U"_0 = 1/2 "V"_0^2 "C"_0`
because here, both charge and capacitance are changed, whereas in equation 4, V0 remains constant. After the dielectric is inserted, the capacitance is increased; hence the stored energy is also increased.
U = `1/2 "CV"_0^2 = 1/2 ε_"r" "CV"_0^2 = ε_"r" "U"_0`
Since er > 1 we have U > U0
It may be noted here that since voltage between the capacitor V0 is constant, the electric field between the plates also remains constant.
APPEARS IN
संबंधित प्रश्न
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports. Show that the capacitance of a spherical capacitor is given by
C = `(4piin_0"r"_1"r"_2)/("r"_1 - "r"_2)`

where r1 and r2 are the radii of outer and inner spheres, respectively.
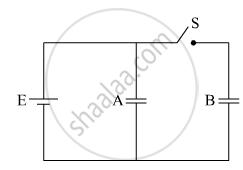
Two identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant K. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
Two identical capacitors of 12 pF each are connected in series across a battery of 50 V. How much electrostatic energy is stored in the combination? If these were connected in parallel across the same battery, how much energy will be stored in the combination now?
Also find the charge drawn from the battery in each case.
A capacitor has capacitance C. Is this information sufficient to know what maximum charge the capacitor can contain? If yes, what is this charges? If no, what other information is needed?
Each of the capacitors shown in figure has a capacitance of 2 µF. find the equivalent capacitance of the assembly between the points A and B. Suppose, a battery of emf 60 volts is connected between A and B. Find the potential difference appearing on the individual capacitors.
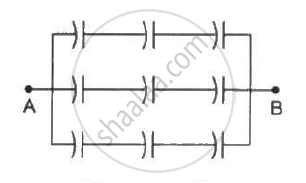
Find the equivalent capacitance of the system shown in figure between the points a and b.

The separation between the plates of a parallel-plate capacitor is 0⋅500 cm and its plate area is 100 cm2. A 0⋅400 cm thick metal plate is inserted into the gap with its faces parallel to the plates. Show that the capacitance of the assembly is independent of the position of the metal plate within the gap and find its value.
Consider an assembly of three conducting concentric spherical shell of radii a, b and c as shown in figure Find the capacitance of the assembly between the points Aand B.

The positive terminal of 12 V battery is connected to the ground. Then the negative terminal will be at ______.
The material filled between the plates of a parallel plate capacitor has a resistivity of 200Ωm. The value of the capacitance of the capacitor is 2 pF. If a potential difference of 40V is applied across the plates of the capacitor, then the value of leakage current flowing out of the capacitor is ______.
(given the value of relative permittivity of a material is 50.)
