Question

Explain the continuity condition for a flow tube. Show that the flow speed is inversely proportional to the cross-sectional area of a flow tube.

Answer 1

Imagine a fluid flowing smoothly or steadily. Although the fluid's velocity in a flow tube is always parallel to the tube, its magnitude might vary. Assume that at points P and Q, the velocity is `vec(v)_1` and `vec(v)_2`, respectively. The mass of the fluid travelling through A₁ in a unit of time is A₁ρ₁v₁, and the mass passing through A₂ in a unit of time is A₂ρ₂v₂, assuming that A₁ and A₂ are the cross-sectional areas of the tube and that ρ₁ and ρ₂ are the fluid densities at these two sites. Since the tube's boundary is closed off to the flow of any fluid, the conservation of mass necessitates

A₁ρ₁v₁ = A₂ρ₂v₂  ...(1)

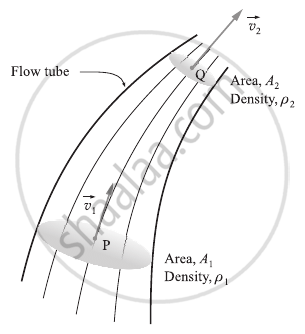
The equation of continuity of flow is represented by equation (1). It is valid for compressible fluids, which, like all gases, can have variable fluid densities at different points along a tube of flow. As with all liquids, an incompressible fluid has the simpler form ρ₁ = ρ₂ Eq. (1).

A₁v₁ = A₂v₂   ...(2)

∴ `v_1/v_2 = A_2/A_1`   ...(3)

that is, the cross-sectional area of a flow tube and the flow speed are inversely related. The flow has a small pace in big areas and vice versa. The continuity equation for an incompressible fluid with constant density over the whole range is given by equation (2).