Advertisements
Advertisements
प्रश्न
Fig. 5 shows a uniform meter scale weighing 200 gf. Provided at its centre. Two weights 300 gf and 500 gf are suspended from the ruler as shown in the diagram. Calculate the resultant torque of the ruler and hence calculate the distance from mid-point where a 100 gf should be suspended to balance the meter scale.

उत्तर
Resultant torque = sum of clockwise moments - sum of anticlockwise moments
Taking, moments about the mid point
Resulttant torque = (300 x 40) - (500 x 20)
or, Resultant torque = 12000 - 10000 = 2000 gf-cm
Let a mass of 100 gf be suspended at a distance 'd' from the mid point towards the right side,
so as to balance the metre scale.
Then, in balanced condition:
sum of clockwise moments = sum of anticlockwise moments
(300 x 40) = (500 x 20) + (100 x d)
or, 12000 = 10000 + 100d
or, 100d = 2000
or,d = 20cm to the right of the mid-point
APPEARS IN
संबंधित प्रश्न
Moment of force = force × perpendicular distance of force – from the pivoted point.
To obtain a given moment of force for turning a body, the force needed can be decreased by
What is thrust?
A rocket is moving at a constant speed in space by burning its fuel and ejecting out the burnt gases through a nozzle. Answer the following
1) Is there any change in the momentum of the rocket? if yes, what causes the change in momentum?
2) Is there any force acting on the rocket? if yes, how much?
Write the expression for calculating the moment of force about a given an axis.
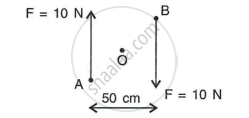
The figure shows two forces each of magnitude 10 N acting at the point A and B at a separation of 50 cm, in opposite directions. Calculate the resultant moment of two forces about the point.
- A,
- B and
- O situated exactly at the middle of the two forces.
What is the work done when no net force is applied on the body?
Calculate the magnitude of the force of a couple, when the arm of the couple is 63 cm and the moment of the couple is 21 Nm.
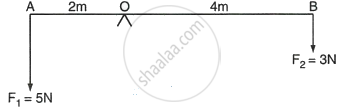
The diagram in Fig shows two forces F1 = 5 N and F2 = 3 N acting at points A and B respectively of a rod pivoted at a point O, such that OA = 2 m and OB = 4 m.
Calculate:
- the moment of force F1 about O.
- the moment of force F2 about O.
- total moment of the two forces about O.
