Advertisements
Advertisements
प्रश्न
Figure shows a charge array known as an electric quadrupole. For a point on the axis of the quadrupole, obtain the dependence of potential on r for r/a >> 1, and contrast your results with that due to an electric dipole, and an electric monopole (i.e., a single charge).

उत्तर
Four charges of same magnitude are placed at points X, Y, Y, and Z respectively, as shown in the following figure.
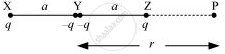
A point is located at P, which is r distance away from point Y.
The system of charges forms an electric quadrupole.
It can be considered that the system of the electric quadrupole has three charges.
Charge +q placed at point X
Charge −2q placed at point Y
Charge +q placed at point Z
XY = YZ = a
YP = r
PX = r + a
PZ = r − a
Electrostatic potential caused by the system of three charges at point P is given by,
`"V" = 1/(4piin_0)["q"/("XP") - (2"q")/("YP") + "q"/("ZP")]`
= `1/(4piin_0)["q"/("r" + "a") - (2"q")/"r" + "q"/("r" - "a")]`
= `"q"/(4piin_0)[("r"("r" - "a") - 2("r" + "a"("r" - "a") + "r"("r" + "a")))/("r"("r" + "a")("r" - "a"))]`
= `"q"/(4piin_0)[("r"^2 - "ra" - 2"r"^2 + 2"a"^2 + "r"^2 + "ra")/("r"("r"^2 - "a"^2))] = "q"/(4piin_0)[(2"a"^2)/("r"("r"^2 - "a"^2))]`
= `(2"qa"^2)/(4piin_0"r"^3(1 - "a"^2/"r"^2))`
Since `"r"/"a"` >> 1,
∴ `"a"/"r" ` << 1
`"a"^2/"r"^2` is taken as negligible.
∴ `"V" = (2"qa"^2)/(4piin_0"r"^3)`
It can be inferred that potential, `"V" prop 1/"r"^3`
However, it is known that for a dipole, `"V" prop 1/"r"^2`
And, for a monopole, `"V" prop 1/"r"`
APPEARS IN
संबंधित प्रश्न
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2 × 10−9 C from a point P (0, 0, 3 cm) to a point Q (0, 4 cm, 0), via a point R (0, 6 cm, 9 cm).
Work done by a uniform electric field 'E' in moving a charge 'q' at a distance 'd' from a to b is ______.
Figure shows some equipotential lines distributed in space. A charged object is moved from point A to point B.
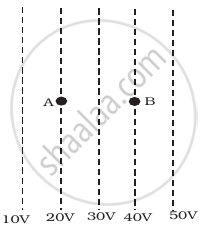 |
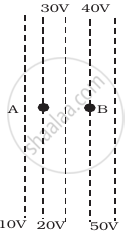 |
 |
| (i) | (ii) | (iii) |
Depict the orientation of an electric dipole in (a) stable and (b) unstable equilibrium in an external uniform electric field. Write the potential energy of the dipole in each case.
