Advertisements
Advertisements
प्रश्न
Find k if x = 3 is a root of equation kx2 – 10x + 3 = 0.
उत्तर
Given x = 3 is a root of equation kx2 – 10x + 3 = 0
So, x = 3 must satisfy the given quadration equation.
k(3)2 – 10(3) + 3 = 0
⇒ 9k - 30 + 3 = 0
⇒ 9k - 27 = 0
⇒ 9k = 27
⇒ k = `27/9`
⇒ k = 3
APPEARS IN
संबंधित प्रश्न
Solve for x :
`1/(x + 1) + 3/(5x + 1) = 5/(x + 4), x != -1, -1/5, -4`
A passenger train takes 3 hours less for a journey of 360 km, if its speed is increased by 10 km/hr from its usual speed. What is the usual speed?
Two natural number differ by 3 and their product is 504. Find the numbers.
Solve the following quadratic equation by factorisation.
7m2 = 21m
Solve the following quadratic equations by factorization:
\[9 x^2 - 6 b^2 x - \left( a^4 - b^4 \right) = 0\]
The positive value of k for which the equation x2 + kx + 64 = 0 and x2 − 8x + k = 0 will both have real roots, is
If 2 is a root of the equation x2 + ax + 12 = 0 and the quadratic equation x2 + ax + q = 0 has equal roots, then q =
If a and b are roots of the equation x2 + ax + b = 0, then a + b =
Solve the following equation:
(2x+3) (3x-7) = 0
Solve the following equation: 4x2 + 16x = 0
Solve the following : `("x" - 1/2)^2 = 4`
The sum of a number and its reciprocal is `2 9/40`. Find the number.
Solve equation using factorisation method:
(2x – 3)2 = 49
Car A travels x km for every litre of petrol, while car B travels (x + 5) km for every litre of petrol.
If car A use 4 litre of petrol more than car B in covering the 400 km, write down and equation in x and solve it to determine the number of litre of petrol used by car B for the journey.
In each of the following, determine whether the given values are solution of the given equation or not:
`x = 1/x = (13)/(6), x = (5)/(6), x = (4)/(3)`
Solve the following equation by factorization
`sqrt(3x + 4) = x`
If the product of two positive consecutive even integers is 288, find the integers.
If the product of two consecutive even integers is 224, find the integers.
Is 0.2 a root of the equation x2 – 0.4 = 0? Justify
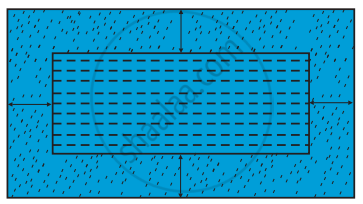
In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m2 [see figure]. Find the length and breadth of the pond.