Advertisements
Advertisements
प्रश्न
Find non singular matrices P & Q such that PAQ is in normal form where A `[[2,-2,3],[3,-1,2],[1,2,-1]]`
उत्तर
Matrix in PAQ form is given by ,
A=P A Q
`[[2,-2,3],[3,-1,2],[1,2,-1]]`=`[[1,0,0],[0,1,0],[0,0,1]] A[[1,0,0],[0,1,0],[0,0,1]] `
`R_1→R_3` ,
`[[1,2,-1],[3,-1,2],[2,-2,-3]] =[[1,0,0],[0,1,0],[0,0,1]] A[[1,0,0],[0,1,0],[0,0,1]] `
`R_2-3R_1,R_3-2R_1`
`[[1,2,-1],[0,-7,5],[0,-6,5]]=[[0,0,1],[0,1,-3],[1,0,-2]] A[[1,0,0],[0,1,0],[0,0,1]] `
𝑪𝟐−𝟐𝑪𝟏,𝑪𝟑+𝑪𝟏,
Now A is in normal form with rank 3.
Compare with PAQ form ,
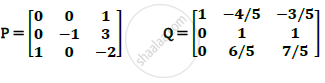
APPEARS IN
संबंधित प्रश्न
Reduce the following matrix to its normal form and hence find its rank.
Investigate for what values of 𝝁 "𝒂𝒏𝒅" 𝝀 the equations : `2x+3y+5z=9`
`7x+3y-2z=8`
`2x+3y+λz=μ`
Have (i) no solution (ii) unique solution (iii) Infinite value
Obtain the root of `x^3-x-1=0` by Newton Raphson Method` (upto three decimal places).
Reduce matrix to PAQ normal form and find 2 non-Singular matrices P & Q.
`[[1,2,-1,2],[2,5,.2,3],[1,2,1,2]]`
