Advertisements
Advertisements
प्रश्न
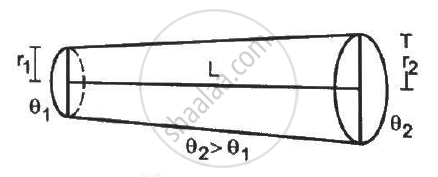
Find the rate of heat flow through a cross section of the rod shown in figure (28-E10) (θ2 > θ1). Thermal conductivity of the material of the rod is K.
उत्तर
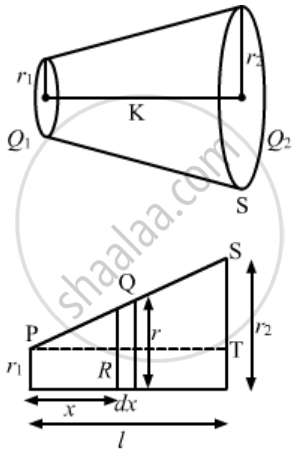
We can infer from the diagram that ΔPQR is similar to ΔPST.
So, by the property of similar triangles,
`x/l = (r - r_1)/(r_2 - r_1)`
⇒ `(r_2 - r_1) x/l = r - r_1`
⇒ `r = r_1 + ( r_2 - r_1 ) x/l`
Let ;
`(r_2 - r_1)/l = a`
⇒ r = ax + r_1................(i)
Thermal resistance is given by
`dR = dx/(K.A)`
⇒ dR = `(dx)/(K.pir^2`]
`dR = (dx)/(K.pi (ax + r_1)^2`
\[\int\limits_0^R\] dR = `1/(kpi)` \[\int\limits_0^l\] `dx/(ax + r_1)`
`R = -(1)/(Kpi) [(1)/(ax + r_1)]_0^6`
`R = -(1)/(aKpi)[(1)/(al + r_1) -1/(r1)]`
`R = -(1)/(aKpi) [ 1/(((r_2 -r_1)/l) l + r_1) - 1/r_1]`
`R = - 1/ (aKpi)[(1)/(r_2)-(1)/(r_1)]`
`R = -(1)/(Kpir_1r_2)`
Rate of flow of heat = `(DeltaQ)/R`
`⇒ q = `( Q_2 - Q_1)/l Kpir_1r_2`
APPEARS IN
संबंधित प्रश्न
A bullet of mass 20 g enters into a fixed wooden block with a speed of 40 m s−1 and stops in it. Find the change in internal energy during the process.
The thermal conductivity of a rod depends on
A uniform slab of dimension 10 cm × 10 cm × 1 cm is kept between two heat reservoirs at temperatures 10°C and 90°C. The larger surface areas touch the reservoirs. The thermal conductivity of the material is 0.80 W m−1 °C−1. Find the amount of heat flowing through the slab per minute.
A liquid-nitrogen container is made of a 1 cm thick styrofoam sheet having thermal conductivity 0.025 J s−1 m−1 °C−1. Liquid nitrogen at 80 K is kept in it. A total area of 0.80 m2 is in contact with the liquid nitrogen. The atmospheric temperature us 300 K. Calculate the rate of heat flow from the atmosphere to the liquid nitrogen.
Water is boiled in a container having a bottom of surface area 25 cm2, thickness 1.0 mm and thermal conductivity 50 W m−1°C−1. 100 g of water is converted into steam per minute in the steady state after the boiling starts. Assuming that no heat is lost to the atmosphere, calculate the temperature of the lower surface of the bottom. Latent heat of vaporisation of water = 2.26 × 106 J kg−1.
Water at 50°C is filled in a closed cylindrical vessel of height 10 cm and cross sectional area 10 cm2. The walls of the vessel are adiabatic but the flat parts are made of 1-mm thick aluminium (K = 200 J s−1 m−1°C−1). Assume that the outside temperature is 20°C. The density of water is 100 kg m−3, and the specific heat capacity of water = 4200 J k−1g °C−1. Estimate the time taken for the temperature of fall by 1.0 °C. Make any simplifying assumptions you need but specify them.
A hollow tube has a length l, inner radius R1 and outer radius R2. The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2 (T2 > T1) (b) the inside of the tube is maintained at temperature T1 and the outside is maintained at T2.
A composite slab is prepared by pasting two plates of thickness L1 and L2 and thermal conductivites K1 and K2. The slabs have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
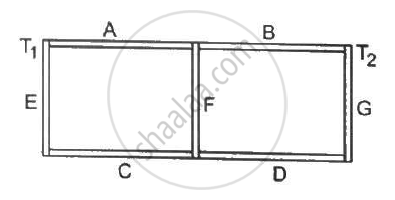
Following Figure shows an aluminium rod joined to a copper rod. Each of the rods has a length of 20 cm and area of cross section 0.20 cm2. The junction is maintained at a constant temperature 40°C and the two ends are maintained at 80°C. Calculate the amount of heat taken out from the cold junction in one minute after the steady state is reached. The conductivites are KAt = 200 W m−1°C−1 and KCu = 400 W m−1°C−1.

The two rods shown in following figure have identical geometrical dimensions. They are in contact with two heat baths at temperatures 100°C and 0°C. The temperature of the junction is 70°C. Find the temperature of the junction if the rods are interchanged.

Seven rods A, B, C, D, E, F and G are joined as shown in the figure. All the rods have equal cross-sectional area A and length l. The thermal conductivities of the rods are KA = KC = K0, KB = KD = 2K0, KE = 3K0, KF = 4K0 and KG = 5K0. The rod E is kept at a constant temperature T1 and the rod G is kept at a constant temperature T2 (T2 > T1). (a) Show that the rod F has a uniform temperature T = (T1 + 2T2)/3. (b) Find the rate of heat flowing from the source which maintains the temperature T2.
A rod of negligible heat capacity has length 20 cm, area of cross section 1.0 cm2 and thermal conductivity 200 W m−1°C−1. The temperature of one end is maintained at 0°C and that of the other end is slowly and linearly varied from 0°C to 60°C in 10 minutes. Assuming no loss of heat through the sides, find the total heat transmitted through the rod in these 10 minutes.
A hollow metallic sphere of radius 20 cm surrounds a concentric metallic sphere of radius 5 cm. The space between the two spheres is filled with a nonmetallic material. The inner and outer spheres are maintained at 50°C and 10°C respectively and it is found that 100 J of heat passes from the inner sphere to the outer sphere per second. Find the thermal conductivity of the material between the spheres.
Two bodies of masses m1 and m2 and specific heat capacities s1 and s2 are connected by a rod of length l, cross-sectional area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t = 0, the temperature of the first body is T1 and the temperature of the second body is T2 (T2 > T1). Find the temperature difference between the two bodies at time t.
An amount n (in moles) of a monatomic gas at an initial temperature T0 is enclosed in a cylindrical vessel fitted with a light piston. The surrounding air has a temperature Ts (> T0) and the atmospheric pressure is Pα. Heat may be conducted between the surrounding and the gas through the bottom of the cylinder. The bottom has a surface area A, thickness x and thermal conductivity K. Assuming all changes to be slow, find the distance moved by the piston in time t.
