Advertisements
Advertisements
प्रश्न
Find the sum of all three-digits natural numbers which are divisible by 13.
उत्तर
All three-digit numbers which are divisible by 13 are 104, 117, 130, 143,.…… 938.
This is an AP in which a = 104, d = (117 – 104) = 13 and l = 938
Let the number of terms be n
Then Tn = 938
⇒ a + (n-1) d = 988
⇒ 104+(n-1) × 13 = 988
⇒13n = 897
⇒ n = 69
∴ Required sum = `n/2 (a+l)`
`= 69/2 [ 104+988] = 69 × 546 = 37674`
Hence, the required sum is 37674.
APPEARS IN
संबंधित प्रश्न
In an AP, the first term is -4, the last term is 29 and the sum of all its terms is 150. Find its common difference.
The sum first 10 terms of an AP is -150 and the sum of its next 10 terms is -550 . Find the AP.
The sum of fist m terms of an AP is ( 4m2 - m). If its nth term is 107, find the value of n. Also, Find the 21st term of this AP.
In a school, students decided to plant trees in and around the school to reduce air pollution. It was decided that the number of trees that each section of each class will plant will be double of the class in which they are studying. If there are 1 to 12 classes in the school and each class has two section, find how many trees were planted by student. Which value is shown in the question?
Which of the following sequences are A.P. ? If they are A.P. find the common difference .
127, 132, 137,...
Observe the adjacent Venn diagram and write the complement of A.
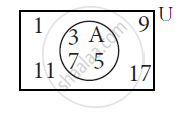
A = {1, 2, 3,4, 5}, B = {5, 6, 7} write AUB .
Write the lower and the uppper class limit of 35 to 40
Solve any four of the following.
If x is the geometric mean of 16 and 9, find x.
First term and common difference of an A.P. are 12 and 4 respectively. If tn = 96 find n.
