Question

Find the area cut off from the parabola 4y = 3x² by the line 2y = 3x + 12.

Answer 1

Equation of parabola: x² = `4/3y` and

Equation of line: y = `(3x + 12)/2`

We eliminate y by solving the equations for the parabola and line.

x² = `4/3*((3x + 12))/2`

∴ x² = 2x + 8

∴ x² – 2x – 8 = 0

∴ (x – 4)(x + 2) = 0

∴ x = 4, x = –2

The parabola and line intersect each other at x = 4 and x = – 2.

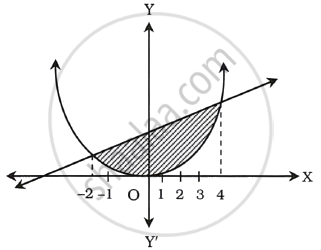
The required area (shaded)

= (Area under the line upto X-axis from x = – 2 to x = 4) – (Area under the parabola upto X-axis from x = – 2 to x = 4)

= `int_-2^4 (3x + 12)/2dx - int_-2^4 (3x^2)/4dx`

= `3/2 int_-2^4 (x + 4)dx - 3/4 int_-2^4 x^2dx`

= `3/2[(x + 4)^2/2]_-2^4 - 3/4[x^3/3]_-2^4`

= `3/4[64 - 4] - 1/4[64 + 8]`

= `3/4(60) - 1/4(72)`

= 45 – 18

= 27 sq. units