Advertisements
Advertisements
प्रश्न
Find the area of a circular pathway whose outer radius is 32 cm and inner radius is 18 cm.
उत्तर
Radius of the outer circle R = 32 cm
Radius of the inner circle r = 18 cm
Area of the circular pathway = π(R2 – r2) sq.units
= `22/7 (32^2 - 18^2) "cm"^2`
= `22/7 xx (32 + 18) xx (32 - 18) "cm"^2`
= `22/7 xx 50 xx 14 "cm"^2`
= 2,200 cm2
Area of the circular pathway = 2,200 cm2
APPEARS IN
संबंधित प्रश्न
The figure shown is the aerial view of the pathway. Find the area of the pathway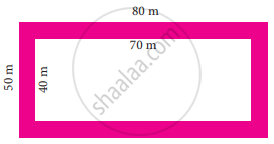
A picture is painted on a ceiling of a marriage hall whose length and breadth are 18 m and 7 m respectively. There is a border of 10 cm along each of its sides. Find the area of the border
A canal of width 1 m is constructed all along inside the field which is 24 m long and 15 m wide. Find (i) the area of the canal (ii) the cost of constructing the canal at the rate of ₹ 12 per sq.m.
The formula used to find the area of the rectangular path is
A path 2 m long and 1 m broad is constructed around a rectangular ground of dimensions 120 m and 90 m respectively. Find the area of the path
A circular path has to be constructed around a circular lawn. If the outer and inner circumferences of the path are 88 cm and 44 cm respectively, find the width and area of the path
A path 5 m wide runs along the inside of the rectangular field. The length of the rectangular field is three times the breadth of the field. If the area of the path is 500 m2 then find the length and breadth of the field
A circular path has to be constructed around a circular ground. If the areas of the outer and inner circles are 1386 m2 and 616 m2 respectively, find the width and area of the path
A strip of 4 cm wide is cut and removed from all the sides of the rectangular cardboard with dimensions 30 cm × 20 cm. Find the area of the removed portion and area of the remaining cardboard
A rectangular field is of dimension 20 m × 15 m. Two paths run parallel to the sides of the rectangle through the centre of the field. The width of the longer path is 2 m and that of the shorter path is 1 m. Find (i) the area of the paths (ii) the area of the remaining portion of the field (iii) the cost of constructing the roads at the rate of ₹ 10 per sq.m
