Question

Find the area of the region lying in the first quadrant and bounded by y = 4x², x = 0, y = 2 and y = 4.

Answer 1

The equation of the curve is y = 4x²,

i.e. x² = `y/4`

∴ x = `sqrt(y)/2`

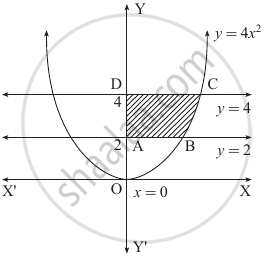
Required area = Area of the region ABCDA

= `int_2^4 x  dy, "where"  x = sqrt(y)/2`

= `int_2^4 sqrt(y)/2dy`

= `1/2 int_2^4 y^(1/2)dy`

= `1/2.[y^(3/2)/(3/2)]_2^4`

= `1/3[y^(3/2)]_2^4`

= `1/3[4^(3/2) - 2^(3/2)]`

= `1/3(8 - 2sqrt(2))` sq units.