Advertisements
Advertisements
प्रश्न
Find the co-ordinates of the circumcentre of the triangle whose vertices are A(– 2, 3), B(6, – 1), C(4, 3).
उत्तर
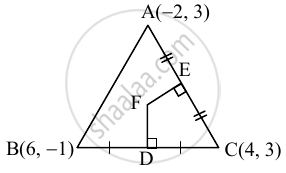
Here, A(– 2, 3), B(6, – 1), C(4, 3) are the verticals of ΔABC.
Let F be the circumcentre of ΔABC.
Let FD and FE be the perpendicular bisectors of the sides BC and AC respectively.
∴ D and E are the midpoints of side BC and AC respectively.
∴ D = `((6 + 4)/2, (-1 + 3)/2)`
∴ D = (5, 1)
and E = `((-2 + 4)/2, (3 + 3)/2)`
∴ E = (1, 3)
Now, slope of BC = `(-1 - 3)/(6 - 4)` = – 2
∴ slope of FD = `1/2` ...[∵ FD ⊥ BC]
Since, FD passes through (5, 1) and has slope `1/2`
∴ Equation of FD is
y – 1 = `1/2(x - 5)`
∴ 2(y – 1) = x – 5
∴ x – 2y – 3 = 0 ....(i)
Since, both the points A and C have same y co-ordinates i.e. 3
∴ the points A and C lie on the line y = 3.
Since, FE passes through E(1, 3).
∴ the equation of FE is x = 1. …(ii)
To find co-ordinates of circumcentre, we have to solve equations (i) and (ii).
Substituting the value of x in (i), we get
1 – 2y – 3 = 0
∴ y = – 1
∴ Co-ordinates of circumcentre F ≡ (1, – 1).
APPEARS IN
संबंधित प्रश्न
Write the equation of the line: parallel to the X-axis and at a distance of 5 units from it and above it.
Write the equation of the line: parallel to the Y-axis and at a distance of 5 units from it and to the left of it.
Obtain the equation of the line: parallel to the X-axis and making an intercept of 3 units on the Y-axis.
Obtain the equation of the line containing the point: B(4, – 3) and parallel to the X-axis.
Show that the lines x – 2y – 7 = 0 and 2x − 4y + 5 = 0 are parallel to each other.
If the line 3x + 4y = p makes a triangle of area 24 square units with the co-ordinate axes, then find the value of p.
Find the distance of the point A(– 2, 3) from the line 12x – 5y – 13 = 0.
Find the distance between parallel lines 9x + 6y − 7 = 0 and 9x + 6y − 32 = 0.
Find the equation of the line passing through the point of intersection of lines x + y – 2 = 0 and 2x – 3y + 4 = 0 and making intercept 3 on the X-axis.
Which of the following lines passes through the origin?
Obtain the equation of the line which is parallel to the Y-axis and 2 units to the left of it.
Obtain the equation of the line which is parallel to the X-axis and making an intercept of 5 on the Y-axis.
Obtain the equation of the line which is: parallel to the Y-axis and making an intercept of 3 on the X-axis.
Obtain the equation of the line containing the point: (2, 3) and parallel to the X−axis.
