Advertisements
Advertisements
प्रश्न
Find the equation of a straight line joining the point of intersection of 3x + y + 2 = 0 and x – 2y – 4 = 0 to the point of intersection of 7x – 3y = – 12 and 2y = x + 3
उत्तर
The given lines are
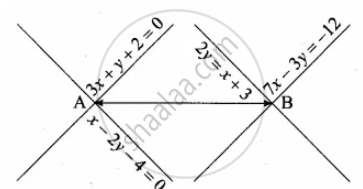
3x + y + 2 = 0
3x + y = − 2 ...(1)
x − 2y − 4 = 0
x − 2y = 4 ...(2)
(1) × 2 ⇒ 6x + 2y = − 4 ...(3)
(2) × 1 ⇒ x − 2y = 4 ...(4)
By adding (3) and (4) ⇒ 7x = 0
x = `0/7` = 0
Substitute the value of x = 0 in (1)
3(0) + y = −2
y = − 2
The point of intersection is (0, −2).
The given equation is
7x − 3y = − 12 ...(5)
2y = x + 3
− x + 2y = 3 ...(6)
(5) × 1 ⇒ 7x − 3y = − 12 ...(7)
(6) × 7 ⇒ − 7x + 14y = 21 ...(8)
By adding (7) and (8) ⇒ 11y = 9
y = `9/11`
Substitute the value of y = `9/11` in (6)
`- x + 2(9/11)` = 3
⇒ `-x + 18/11` = 3
− x = `3 - 18/11`
= `(33 - 18)/11`
= `15/11`
x = `- 15/11`
The point of intersection is `(- 15/11, 9/11)`
Equation of the line joining the points (0, −2) and `(- 15/11, 9/11)` is
`(y - y_1)/(y_2 - y_1) = (x - x_1)/(x_2 - x_1)`
`(y + 2)/(9/11 + 2) = (x - 0)/(- 15/11 - 0)`
`(y+ 2)/(9 / 11 + 2) = x/(- 15/11)`
`(y + 2)/(31/11) = - (11x)/15`
⇒ `(y + 2) 11/31 = - (11x)/15`
31 × (– 11x) = 11 × 15 (y + 2)
= 165 (y + 2)
– 341x = 165y + 330
– 341x – 165y – 330 = 0
341x + 165y + 330 = 0
⇒ 31x + 15y + 30 = 0 ...(÷ by 11)
The required equation is 31x + 15y + 30 = 0
APPEARS IN
संबंधित प्रश्न
Find the slope of the line which is parallel to y = 0.7x – 11
Find the slope of the line which is perpendicular to the line x = – 11
Check whether the given lines are parallel or perpendicular
5x + 23y + 14 = 0 and 23x – 5x + 9 = 0
If the straight lines 12y = − (p + 3)x + 12, 12x – 7y = 16 are perpendicular then find ‘p’
A(−3, 0) B(10, −2) and C(12, 3) are the vertices of ∆ABC. Find the equation of the altitude through A and B.
Find the equation of a straight line through the intersection of lines 7x + 3y = 10, 5x – 4y = 1 and parallel to the line 13x + 5y + 12 = 0
Find the equation of a straight line through the point of intersection of the lines 8x + 3y = 18, 4x + 5y = 9 and bisecting the line segment joining the points (5, −4) and (−7, 6)
The straight line given by the equation x = 11 is
The equation of a line passing through the origin and perpendicular to the line 7x − 3y + 4 = 0 is
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
