Advertisements
Advertisements
प्रश्न
Find the number of ways for 15 people to sit around the table so that no two arrangements have the same neighbours
उत्तर
There are 15 people to sit around a table.
∴ They can be arranged in (15 – 1)! = 14! ways.
But, they should not have the same neighbour in any two arrangements.
Around table, arrangements (i.e. clockwise and anticlock wise) coincide.
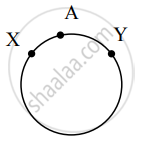
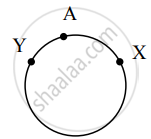
∴ No. of arrangements possible for not to have same neighbours = `(14!)/2`
APPEARS IN
संबंधित प्रश्न
In how many different ways can 8 friends sit around a table?
A party has 20 participants and a host. Find the number of distinct ways for the host to sit with them around a circular table. How many of these ways have two specified persons on either side of the host?
Find the number of ways for 15 people to sit around the table so that no two arrangements have the same neighbours.
Find the number of sitting arrangements for 3 men and 3 women to sit around a table so that exactly two women are together.
Four objects in a set of ten objects are alike. Find the number of ways of arranging them in a circular order.
In how many different ways can 8 friends sit around a table?
A party has 20 participants. Find the number of distinct ways for the host to sit with them around a circular table. How many of these ways have two specified persons on either side of the host?
Delegates from 24 countries participate in a round table discussion. Find the number of seating arrangments where two specified delegates are always together
A committee of 10 members sits around a table. Find the number of arrangements that have the president and the vice-president together.
Five men, two women, and a child sit around a table. Find the number of arrangements where the child is seated between the two women
Five men, two women, and a child sit around a table. Find the number of arrangements where the child is seated between two men
Eight men and six women sit around a table. How many of sitting arrangements will have no two women together?
Find the number of seating arrangements for 3 men and 3 women to sit around a table so that exactly two women are together.
Four objects in a set of ten objects are alike. Find the number of ways of arranging them in a circular order
Fifteen persons sit around a table. Find the number of arrangements that have two specified persons not sitting side by side.
Answer the following:
There are 12 distinct points A, B, C, ....., L, in order, on a circle. Lines are drawn passing through each pair of points how many lines are there in total.
Answer the following:
There are 12 distinct points A, B, C, ....., L, in order, on a circle. Lines are drawn passing through each pair of points how many lines pass through D.
Answer the following:
There are 12 distinct points A, B, C, ....., L, in order, on a circle. Lines are drawn passing through each pair of points how many triangles are determined by lines.
Answer the following:
There are 12 distinct points A, B, C, ....., L, in order, on a circle. Lines are drawn passing through each pair of points how many triangles have on vertex C.
A group of 5 men and 4 women are arranged at random, one after the other. The probability that women and men occupy alternate seats is ______
The number of ways in which 51 books can be distributed among three students, each receiving 17 books, is ______
