Question

For changing the capacitance of a given parallel plate capacitor, a dielectric material of dielectric constant K is used, which has the same area as the plates of the capacitor.

The thickness of the dielectric slab is `3/4`d, where 'd' is the separation between the plate of the parallel plate capacitor.

The new capacitance (C') in terms of the original capacitance (C₀) is given by the following relation:

विकल्प

• C' = `(4"K")/("K"+3)"C"_0`

• C' = `4/(3+"K")"C"_0`

• C' = `(3+"K")/(4"K")"C"_0`

• C' = `(4+"K")/4"C"_0`

Answer 1

`bb("C"^' = (4"K")/("K"+3)"C"_0)`

Explanation:

The expression of a parallel place capacitor

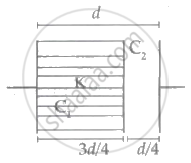
Here, `"C"_0 = ("A"epsilon_0)/"d"`

So, `"C"_1 = ("KA"epsilon_0)/((3"d")/4)`   .....at d →`(3"d")/4`

And `"C"_2 = ("A"epsilon_0)/("d"/4)`      ....at d →`"d"/4`

Now equivalent capacitance

C' = `("C"_1"C"_2)/("C"_1+"C"_2)`

⇒ `((4"K"("A"epsilon_0)/(3"d"))(4("A"epsilon_0)/"d"))/(4"K"("A"epsilon_0)/(3"d")+4("A"epsilon_0)/"d")`

⇒ `((4"KA"^2epsilon_0^2)/(3"d"^2)xx4)/((4"A"epsilon_0)/"d"["K"/3+1])`

⇒ `(4"K")/((3+"K"))"C"_0`