Question

Four identical particles of mass M are located at the corners of a square of side 'a'. What should be their speed if each of them revolves under the influence of the other's gravitational field in a circular orbit circumscribing the square?

विकल्प

• `1.35sqrt((GM)/a)`

• `1.16sqrt((GM)/a)`

• `1.21sqrt((GM)/a)`

• `1.41sqrt((GM)/a)`

Answer 1

`underlinebb(1.16sqrt((GM)/a))`

Explanation:

Given: M is the mass of four identical particles placed at the four corners of a square. square edge length = a, Under the influence of each other's gravitational field, the particles revolve in a circular path. 

To find: The speed of particles.

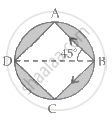
The net force on a particle of mass M located at position B will be directed toward the circle's centre:

F_net = F_BD + F_BA cos45° + F_CA cos45°

= `(GM^2)/(sqrt2a)^2 + (GM^2)/a^2(1/sqrt2) + (GM^2)/a^2(1/sqrt2)`

Square body diagonal BD = `sqrt2`a.

F_net = `(GM^2)/a^2(1/2 + sqrt2)` ....(i)

Equation (i) represents the net force acting on a particle located at B. It has a centrifugal force.

`(Mv^2)/(a/sqrt2) = (GM^2)/a^2(1/2 + sqrt2)`

`("the distance between location B and the centre of the square is" a/sqrt2).`

`v^2 = (GM)/a(1/(2sqrt2) + 1);`

`v = 1.16sqrt((GM)/a)`