Advertisements
Advertisements
प्रश्न
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: n(C ∩ D)
उत्तर
Here,
A= {1, 2, 3, 4, 5, 6, 7, 8, 9}
B = {P, U, E, T}
C = {0, 1, 4, 9}
D = { } or Φ
C ∩ D = { }
n(C ∩ D) = 0
APPEARS IN
संबंधित प्रश्न
State, whether the pair of sets, given below, are equal sets or equivalent sets:
{3, 5, 7} and {5, 3, 7}
Write the cardinal number of the following set:
C = { }
Given:
A = {Natural numbers less than 10}
B = {Letters of the word ‘PUPPET’}
C = {Squares of first four whole numbers}
D = {Odd numbers divisible by 2}.
Find: A ∩ C AND n(A ∩ C)
If U = {x : x ∈ N, x ≤ 10}, A = {2, 3, 4, 8, 10} and B = {1, 2, 5, 8, 10}, then verify that n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Verify n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C) for the following sets
A = {1, 3, 5}, B = {2, 3, 5, 6}, C = {1, 5, 6, 7}
In a colony, 275 families buy Tamil newspaper, 150 families buy English newspaper, 45 families buy Hindi newspaper, 125 families buy Tamil and English newspaper, 17 families buy English and Hindi newspapers, 5 families buy Tamil and Hindi newspaper and 3 families buy all the three newspaper. If each family buy atleast one of these newspaper then find Number of families buy only one newspaper
For any three sets A, B and C, (A – B) ∩ (B – C) is equal to
If J = Set of three sided shapes, K = Set of shapes with two equal sides and L = Set of shapes with right angle, then J ∩ K ∩ L is
The shaded region in the Venn diagram is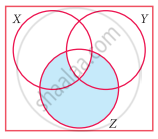
In a city, 40% people like only one fruit, 35% people like only two fruits, 20% people like all the three fruits. How many percentage of people do not like any one of the above three fruits?
