Advertisements
Advertisements
प्रश्न
How many numbers formed with the digits 0, 1, 2, 5, 7, 8 will fall between 13 and 1000 if digits can be repeated?
उत्तर
Case I: 2-digit numbers more than 13, less than 20, formed from the digits 0, 1, 2, 5, 7, 8
Number of such numbers = 3
Case II: 2-digit numbers more than 20 formed from 0, 1, 2, 5, 7, 8
Using multiplication principle, the number of such numbers (repetition allowed)
= 4 × 6
= 24
Case III: 3-digit numbers formed from 0, 1, 2, 5, 7, 8
Using multiplication principle, the number of such numbers (repetition allowed)
= 5 × 6 × 6
= 180
All cases are mutually exclusive.
Required number = 3 + 24 + 180 = 207
APPEARS IN
संबंधित प्रश्न
How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is allowed?
A teacher wants to select the class monitor in a class of 30 boys and 20 girls. In how many ways can the monitor be selected if the monitor must be a girl or a boy?
How many two letter words can be formed using letters from the word SPACE, when repetition of letters is allowed?
How many three-digit numbers can be formed from the digits 0, 1, 3, 5, 6 if repetitions of digits are not allowed?
How many numbers between 100 and 1000 have 4 in the units place?
How many numbers between 100 and 1000 have the digit 7 exactly once?
How many four digit numbers will not exceed 7432 if they are formed using the digits 2, 3, 4, 7 without repetition?
How many five-digit numbers formed using the digit 0, 1, 2, 3, 4, 5 are divisible by 5 if digits are not repeated?
Select the correct answer from the given alternatives.
A college offers 5 courses in the morning and 3 in the evening. The number of ways a student can select exactly one course, either in the morning or in the evening
Select the correct answer from the given alternatives.
A college has 7 courses in the morning and 3 in the evening. The possible number of choices with the student if he wants to study one course in the morning and one in the evening is -
How many words can be formed by writing letters in the word CROWN in different order?
Answer the following:
A hall has 12 lamps and every lamp can be switched on independently. Find the number of ways of illuminating the hall.
A person went to a restaurant for dinner. In the menu card, the person saw 10 Indian and 7 Chinese food items. In how many ways the person can select either an Indian or a Chinese food?
There are 3 types of toy car and 2 types of toy train available in a shop. Find the number of ways a baby can buy a toy car and a toy train?
Three persons enter into a conference hall in which there are 10 seats. In how many ways they can take their seats?
How many three-digit numbers are there with 3 in the unit place?
without repetition
How many three-digit odd numbers can be formed by using the digits 0, 1, 2, 3, 4, 5? if the repetition of digits is allowed
How many three-digit numbers, which are divisible by 5, can be formed using the digits 0, 1, 2, 3, 4, 5 if repetition of digits are not allowed?
In how many ways 10 pigeons can be placed in 3 different pigeon holes?
Find the value of `(("n" + 3)!)/(("n" + 1)!)`
Evaluate `("n"!)/("r"!("n" - "r")!)` when n = 10, r = 3
Find the value of n if `1/(8!) + 1/(9!) = "n"/(10!)`
Choose the correct alternative:
The sum of the digits at the 10th place of all numbers formed with the help of 2, 4, 5, 7 taken all at a time is
Choose the correct alternative:
In an examination there are three multiple choice questions and each question has 5 choices. Number of ways in which a student can fail to get all answer correct i
Choose the correct alternative:
The number of 5 digit numbers all digits of which are odd i
Choose the correct alternative:
The number of five digit telephone numbers having at least one of their digits repeated i
Choose the correct alternative:
The number of 10 digit number that can be written by using the digits 2 and 3 is
In a class, there are 27 boys and 14 girls. The teacher wants to select 1 boy and 1 girl to represent the class for a function. In how many ways can the teacher make this selection?
In how many ways can this diagram be coloured subject to the following two conditions?
(i) Each of the smaller triangle is to be painted with one of three colours: red, blue or green.
(ii) No two adjacent regions have the same colour.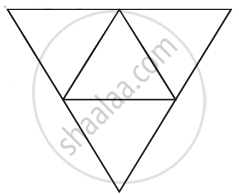
A candidate is required to answer 7 questions out of 12 questions, which are divided into two groups, each containing 6 questions. He is not permitted to attempt more than 5 questions from either group. Find the number of different ways of doing question
The number of possible outcomes when a coin is tossed 6 times is ______.
The sum of the digits in unit place of all the numbers formed with the help of 3, 4, 5 and 6 taken all at a time is ______.
