Question

If a cone is cut into two parts by a horizontal plane passing through the mid-point of its axis, the axis, the ratio of the volumes of upper and lower part is

विकल्प

• 1 : 2

•  2 : 1

• 1: 7

• 1 : 8

Answer 1

If a cone is cut into two parts by a plane parallel to the base, the portion that contains the base is called the frustum of a cone

 

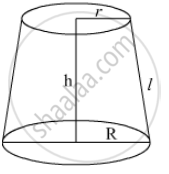
Let ‘r’ be the top radius

‘R’ be the radius of the base

‘h’ be the height of the frustum

‘l’ be the slant height of the frustum.

‘H’ be the height of the complete cone from which the frustum is cut

Then from similar triangles we can write the following relationship

`r/R = (H-h)/H`

Here, since the plane passes through the midpoint of the axis of the cone we have

H = 2 h

Substituting this in the earlier relationship we have

`r/R=(2h-h)/2h`

`r/R = h/2h`

`r/R = 1/2`

`R = 2r`

The volume of the entire cone with base radius ‘R’ and vertical height ‘H’ would be

Volume of the uncut cone = `1/3 piR^2 H`

Replacing R = 2r  and H = 2 h in the above equation we get

Volume of the uncut cone = `1/3 pi(2r)^2(2h)`

= `8/3 pir^2h`

Volume of the smaller cone − the top part after the original cone is cut − with base radius ‘r’ and vertical height ‘h’ would be

Volume of the top part= `1/3pir^2h`

Now, the volume of the frustum − the bottom part after the original cone is cut − would be,

Volume of the bottom part= Volume of the uncut cone − Volume of the top part after the cone is cut

= `8/3pir^2h - 1/3 pir^2h`

Volume of the bottom part= `7/3 pi r^2 h`

Now the ratio between the volumes of the top part and the bottom part after the cone is cut would be,

`("Volume of the top part  ")/("Volume of the bottom part")=((3) pir^2h)/((3)(7)pir^2h)`

`("Volume of the top part")/("Volume of the bottom part") = 1/7`