Question

In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.

विकल्प

• None of these

• 9.6 cm

• 10.8 cm

• 4.8 cm

Answer 1

9.6 cm

Explanation:

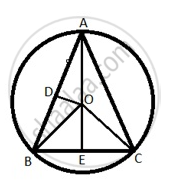
Consider the triangles OAB and OAC are congruent as

AB = AC

OA is common.

OB = OC = 5cm.

So ∠OAB = ∠OAC

Draw OD perpendicular to AB

Hence AD = `"AB"/2 = 6/2` = 3 cm as the perpendicular to the chord from the center bisects the chord.

In ΔADO

OD² = AO² - AD²

OD² = 5² - 3²

OD = 4 cm

So Area of OAB = `1/2 "AB" xx "OD" = 1/2 6 xx 4` = 12 sq. cm. ….. (i)

Now AO extended should meet the chord at E and it is middle of the BC as ABC is an isosceles with AB = AC.

Triangles AEB and AEC are congruent as

AB = AC

AE common,

∠OAB = ∠OAC.

Therefore triangles being congruent, ∠AEB = ∠AEC = 90°

Therefore BE is the altitude of the triangle OAB with AO as base.

Also this implies BE = EC or BC = 2BE

Therefore the area of the ΔOAB

= `1/2 × "AO" × "BE" = 1/2 × 5 × "BE"` = 12 sq. cm as arrived in eq (i).

BE = `12 × 2/5` = 4.8 cm

Therefore BC = 2BE = 2 × 4.8 cm = 9.6 cm.