Advertisements
Advertisements
प्रश्न
In a test on 2,000 electric bulbs, it was found that bulbs of a particular make, was normally distributed with an average life of 2,040 hours and standard deviation of 60 hours. Estimate the number of bulbs likely to burn for more 1,920 hours but less than 2,100 hours
उत्तर
Let x denote the burning of the bulb follows normal distribution with mean 2,040 and standard deviation 60 hours.
Here m = 2040
σ = 60
N = 2000
The standard normal variate
z = `(x - mu)/sigma`
= `(x - 2040)/60`
P(more 1,920 hours but less than 2,100 hours)
= P(1920 < x < 2100)
When x = 1950
z = `(1920 - 2040)/60`
= `(-120)/60`
= – 2
z = `(2100 - 2040)/60`
= `(-60)/60`
= – 2
∴ P(1920 < x < 2040) = P(– 2 < z < 1)
= P(0 < z < 2) + P(0 < z < 1)
= 0.4772 + 0.3413
= 0.8185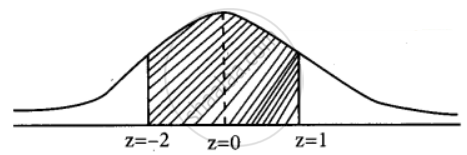
∴ Number of bulbs whose burning time more than 1920 hours but less than 2100 hours)
= 0.8185 × 2000
= 1637
APPEARS IN
संबंधित प्रश्न
If the probability of success is 0.09, how many trials are needed to have a probability of atleast one success as 1/3 or more?
Among 28 professors of a certain department, 18 drive foreign cars and 10 drive local made cars. If 5 of these professors are selected at random, what is the probability that atleast 3 of them drive foreign cars?
Out of 750 families with 4 children each, how many families would be expected to have atmost 2 girls
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of 2 successes
Derive the mean and variance of poisson distribution
The average number of phone calls per minute into the switchboard of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be exactly 3 calls
Choose the correct alternative:
If X ~ N(µ, σ2), the maximum probability at the point of inflexion of normal distribution
Choose the correct alternative:
In a parametric distribution the mean is equal to variance is
Choose the correct alternative:
The starting annual salaries of newly qualified chartered accountants (CA’s) in South Africa follow a normal distribution with a mean of ₹ 180,000 and a standard deviation of ₹ 10,000. What is the probability that a randomly selected newly qualified CA will earn between ₹ 165,000 and ₹ 175,000?
Choose the correct alternative:
In a large statistics class, the heights of the students are normally distributed with a mean of 172 cm and a variance of 25 cm. What proportion of students is between 165cm and 181 cm in height?
