Question

In ΔABC, ∠ACB = 90° and CD ⊥ AB. 

Prove that : `(BC^2)/(AC^2)=(BD)/(AD)`

Answer 1

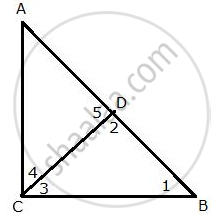
In ΔCDB,
∠1 + ∠2 + ∠3 = 180°
∠1 + ∠3 = 90°… (1) (Since, ∠2 = 90°)  
∠3 + ∠4 = 90° … (2) (Since, ∠ACB = 90°)
From (1) and (2),
∠1 + ∠3 = ∠3 + ∠4
∠1 = ∠4
Also, ∠ADC = ∠ACB = 90°
∴ΔACD ~ ΔABC (AA similarity)

`(AC)/(AB)=(AD)/(AC)`

`AC^2=AB xx AD ............................................ (1)`
Now ∠BDC = ∠ACB = 90°

∠CBD = ∠ABC (common)

∆BCD ~ ∆ BAC (AA similarity)
`∴ (BC)/(BA)=(BD)/(BC)....................................(2)`

`BC^2 = BA × BD`
From (1)and (2), we get,
`(BC^2)/(AC^2)=(BA xx BD)/(AB xx AD)= (BD)/(AD)`