Question

In ∆ ABC, ∠B = 2 ∠C and the bisector of angle B meets CA at point D. Prove that:
(i) ∆ ABC and ∆ ABD are similar,
(ii) DC: AD = BC: AB

Answer 1

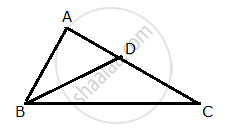
(i) Since, BD is the bisector of angle B,

∠ABD = ∠DBC
Also, given ∠B =2∠C
∴∠ABD = ∠DBC = ∠ACB .... (1)
In ∆ ABC and ∆ ABD,
∠BAC = ∠DAB (Common)
∠ACB = ∠ABD (Using (1))
∴∆ABC ~ ∆ADB (By AA similarity)

(ii) Since, triangles ABC and ADB are similar,

`∴ ("BC")/("BD")=("AB")/("AD")`

`("BC")/("AB")=("BD")/("AD")`

`("BC")/("AB")=("DC")/("AD")     (∠"DBC" = ∠"'DCB" ⇒ "DC" = "BD")`

`"BC" : "AB" = "DC" : "AD"`