Advertisements
Advertisements
प्रश्न
In ∆ABC, DE is parallel to base BC, with D on AB and E on AC. If `\frac{AD}{DB}=\frac{2}{3}` , find `\frac{BC}{DE}.`
योग
उत्तर
In ∆ABC, we have
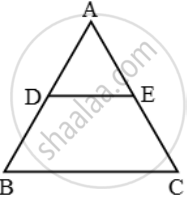
DE || BC `\Rightarrow \frac{AB}{AD}=\frac{AC}{AE}`
Thus, in triangles ABC and ADE, we have
`\frac{AB}{AD}=\frac{AC}{AE} ` and, ∠A = ∠A
Therefore, by SAS-criterion of similarity, we have
∆ABC ~ ∆ADE
`\Rightarrow \frac{AD}{AD}=\frac{BC}{DE} ….(i)`
It is given that
`\frac{AD}{DB}=\frac{2}{3} `
`\Rightarrow \frac{DB}{AD}=\frac{3}{2}`
`\Rightarrow \frac{DB}{AD}+1=\frac{3}{2}+1`
`\Rightarrow \frac{DB+AD}{AD}=\frac{5}{2}`
`\Rightarrow \frac{AB}{DE}=\frac{5}{2} ….(ii)`
From (i) and (ii), we get
`\frac{BC}{DE}=\frac{5}{2}`
shaalaa.com
क्या इस प्रश्न या उत्तर में कोई त्रुटि है?
