Advertisements
Advertisements
рдкреНрд░рд╢реНрди
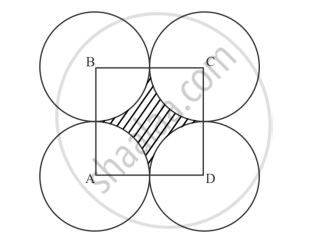
In below Fig., points A, B, C and D are the centers of four circles that each have a radius of length one unit. If a point is selected at random from the interior of square ABCD. What is the probability that the point will be chosen from the shaded region?
рдЙрддреНрддрд░
Radius of circle = 1cm
Length of side of square = 1 + 1 = 2cm
Area of square = 2 × 2 =` 4cm^2`
Area of shaded region = area of square – 4 × area of quadrant
= 4 – 4 `(1/4) pi(1)^2`
= (4 − ЁЭЬЛ)` cm^2`
Probability that the point will be chosen from the shaded region =`"Area of shaded regfion"/"Area of square ABCD"`= `(4−pi)/4` = 1 −`(pi/4)`
Since geometrical probability,
P(E) =`"Measure of specified part of region"/"Measure of the whole region"`
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
Cards marked with number 3, 4, 5, ...., 50 are placed in a box and mixed thoroughly. A card is drawn at random form the box. Find the probability that the selected card bears a perfect square number.
All the black face cards are removed from a pack of 52 playing cards. The remaining cards are well shuffled and then a card is drawn at random. Find the probability of getting a:
(i) face card
(ii) red card
(iii) black card
(iv) king
Cards numbered from 11 to 60 are kept in a box. If a card is drawn at random from the box, find the probability that the number on the drawn card is a perfect square number.
A group consists of 12 persons, of which 3 are extremely patient, other 6 are extremely honest and rest are extremely kind. A person form the group is selected at random. Assuming that each person is equally likely to be selected, find the probability of selecting a person who is extremely patient
All the black face cards are removed from a pack of 52 cards. The remaining cards are well shuffled and then a card is drawn at random. Find the probability of getting king
In a bag there are 44 identical cards with figure of circle or square on them. There are 24 circles, of which 9 are blue and rest are green and 20 squares of which 11 are blue and rest are green. One card is drawn from the bag at random. Find the probability that it has the figure of
In a single throw of a pair of dice, the probability of getting the sum a perfect square is
A bag contains 18 balls out of which x balls are red. If the ball is drawn at random from the bag, what is the probability that it is not red?
A bag contains 18 balls out of which x balls are red. If two more red balls are put in the bag, the probability of drawing a red ball will be `9/8` times the probability of drawing a red ball in the first case. Find the value of x.
Once card is drawn at random from a well-shuffled deck of 52 cards. What is the probability of getting a black face card?
Three identical coins are tossed together. What is the probability of obtaining:
no head?
Two coins are tossed together. Find the probability of getting: at most one head:
A coin is tossed once. Find the probability of getting a head
There are 24 balls in a pot. If 3 of them are Red, 5 of them are Blue and the remaining are Green then, what is the probability of picking out a Blue ball?
Two dice are rolled, find the probability that the sum is equal to 4
Ram put some buttons on the table. There were 4 blue, 7 red, 3 black and 6 white buttons in all. All of a sudden, a cat jumped on the table and knocked out one button on the floor. What is the probability that the button on the floor is blue?
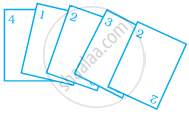
Rohan and Shalu are playing with 5 cards as shown in the figure. What is the probability of Rohan picking a card without seeing, that has the number 2 on it?
To verify pythagoras theorem is a random experiment.
Ritwik draws a ball from a bag that contains white and yellow balls. The probability of choosing a white ball is `2/9`. If the total number of balls in the bag is 36, find the number of yellow balls.
Sonia picks up a card from the given cards.
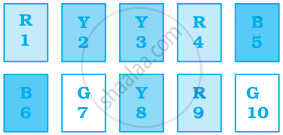
Calculate the probability of getting B card bearing number > 7
