Advertisements
Advertisements
प्रश्न
In the following, the coordinates of the three vertices of a rectangle ABCD are given. By plotting the given points; find, in case, the coordinates of the fourth vertex:
A(2, 0), B(8, 0) and C(8, 4).
उत्तर
A(2, 0), B(8, 0) and C(8, 4).
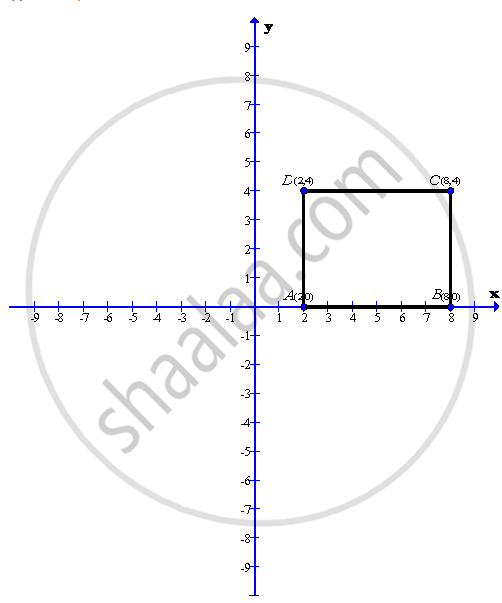
After plotting the given points A(2,0), B(8,0) and C(8,4) on a graph paper; joining A with B and B with C. From the graph it is clear that the vertical distance between the points B(8,0) and C(8,4) is 4 units, therefore the vertical distance between the points A(2,0) and D must be 4 units. Now complete the rectangle ABCD
As is clear from the graph D(2,4)
APPEARS IN
संबंधित प्रश्न
Use the graph given alongside, to find the coordinates of the point (s) satisfying the given condition:
(i) The abscissa is 2.
(ii)The ordinate is 0.
(iii) The ordinate is 3.
(iv) The ordinate is -4.
(v) The abscissa is 5.
(vi) The abscissa is equal to the ordinate.
(vii) The ordinate is half of the abscissa.

In the following, the coordinates of the three vertices of a rectangle ABCD are given. By plotting the given points; find, in case, the coordinates of the fourth vertex:
A (4, 2), B(-2, 2) and D(4, -2).
In the following, the coordinates of the three vertices of a rectangle ABCD are given. By plotting the given points; find, in case, the coordinates of the fourth vertex:
A (- 4, - 6), C(6, 0) and D(- 4, 0).
In the following, the coordinates of the three vertices of a rectangle ABCD are given. By plotting the given points; find, in case, the coordinates of the fourth vertex:
B (10, 4), C(0, 4) and D(0, -2).
A (-2, 4), C(4, 10) and D(-2, 10) are the vertices of a square ABCD. Use the graphical method to find the co-ordinates of the fourth vertex B. Also, find:
(i) The co-ordinates of the mid-point of BC;
(ii) The co-ordinates of the mid-point of CD and
(iii) The co-ordinates of the point of intersection of the diagonals of the square ABCD.
Draw a graph of each of the following equations: x + 5 = 0
Draw a graph of each of the following equations: 2y - 5 = 0
Draw a graph of each of the following equations: x = 0
Draw a graph of each of the following equations: y = 3
Consider the number of angles of a convex polygon and the number of sides of that polygon. Tabulate as follows:
| Name of Polygon | No. of angles | No. of sides |
Use this to draw a graph illustrating the relationship between the number of angles and the number of sides of a polygon
