Advertisements
Advertisements
प्रश्न
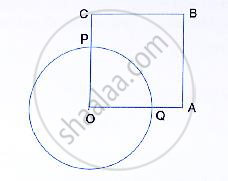
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
उत्तर
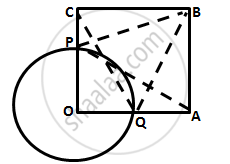
(i)
In ΔOPA and ΔOQC,
OP = OQ (radii of same circle)
∠AOP = ∠COQ (both 90°)
OA = OC (Sides of the square)
By Side – Angle – Side criterion of congruence,
∴ ΔOPA ≅ ΔOQC (by SAS)
(ii)
Now, OP = OQ (radii)
And OC = OA (sides of the square)
∴ OC – OP = OA – OQ
⇒ CP = AQ …………… (1)
In ΔBPC and ΔBQA,
BC = BA (Sides of the square)
∠PCB = ∠QAB (both 90°)
PC = QA (by (1))
By Side – Angle – Side criterion of congruence,
∴ ΔBPC ≅ ΔBQA (by SAS)
shaalaa.com
क्या इस प्रश्न या उत्तर में कोई त्रुटि है?
