Question

In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB)=3/2`

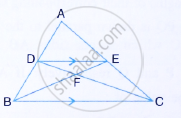
(1) Determine the ratios `(AD)/(AB) and (DE)/(BC)`

(2 ) Prove that ∆DEF is similar to ∆CBF Hence, find `(EF)/(FB)`.

(3) What is the ratio of the areas of ∆DEF and ∆BFC.

Answer 1

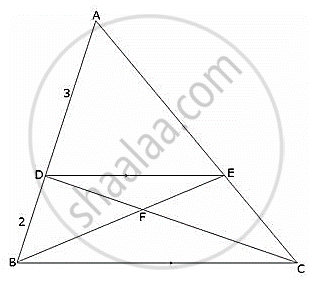
(i) Given, `DE || BC and (AD)/(DB)=3/2`
In ∆ADE and ∆ABC,
∠A = ∠A(Corresponding Angles)
∠ADE = ∠ABC(Corresponding Angles)
∴ ∆ADE ~ ∆ABC (By AA- similarity)
`(AD)/(AB)=(AE)/(AC)=(DE)/(BC)...............................(1)`
Now`(AD)/(AB)=(AD)/(AD+DB)=3/(3+2)=3/5`

`"Using (1), we get"(AD)/(AE)=3/5=(DE)/(BC)`       ....................(2)

(ii) ΔIn DEF and ΔCBF,
∠FDE =∠ FCB(Alternate Angle)
∠DFE = ∠BFC(Vertically Opposite Angle)
∴∆ DEF ~ ∆CBF (By AA- similarity)
`(EF)/(FB)=(DE)/(BC)=3/5     Using (2)`
`(EF)/(FB)=3/5`

(iii) Since the ratio of the areas of two similar triangles is equal to the square of the ratio
of their
corresponding sides, therefore.

`("Area of ΔDFE")/("Area of Δ CBF")=(EF^2)/(FB^2)=(3^2)/(5^2)=9/25`