Question

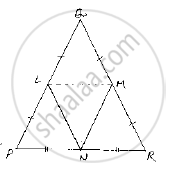
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that LN = MN. 

 

Answer 1

Given that in , ΔPQR, PQ= QR  and ,L M and N are mid-points of PQ, QR and RP respectively 

We have to prove LN = MN. 

Join L and M, M and N, N and L 

We have  

PL =LQ,QM =MR and RN = NP 

[ ∵L,M and N are mid-points of PQ, QR and RP respectively] 

And also 

PQ=QR⇒PL=LQ=QM=MR=`(PQ)/2=(QR)/2`       ........(1) Using mid-point 

theorem, we have  

`MN ll PQ and MN=1/2PQ⇒ MN=PL=LQ`   .........(2) 

Similarly, we have 

`LN ll QR and LN=1/2QR ⇒ LN=QM=MR` ...........(3) 

From equation (1), (2) and (3), we have 

PL=LQ=QM=MR=MN=LN 

∴LN=MN

 

Answer 2

Given that in , ΔPQR, PQ= QR  and ,L M and N are mid-points of PQ, QR and RP respectively 

We have to prove LN = MN. 

Join L and M, M and N, N and L 

We have  

PL =LQ,QM =MR and RN = NP 

[ ∵L,M and N are mid-points of PQ, QR and RP respectively] 

And also 

PQ=QR⇒PL=LQ=QM=MR=`(PQ)/2=(QR)/2`       ........(1) Using mid-point 

theorem, we have  

`MN ll PQ and MN=1/2PQ⇒ MN=PL=LQ`   .........(2) 

Similarly, we have 

`LN ll QR and LN=1/2QR ⇒ LN=QM=MR` ...........(3) 

From equation (1), (2) and (3), we have 

PL=LQ=QM=MR=MN=LN 

∴LN=MN