Question

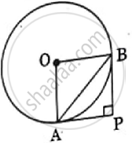
In the adjoining figure, PA and PB are tangents to a circle with centre O such that ∠P = 90°. If AB = `3sqrt2` cm, then the diameter of the circle is ______.

विकल्प

• `3sqrt2` cm

• `6sqrt2` cm

• 3 cm

• 6 cm

Answer 1

In the adjoining figure, PA and PB are tangents to a circle with centre O such that ∠P = 90°. If AB = `3sqrt2` cm, then the diameter of the circle is 6 cm.

Explanation:

Given:

• PA and PB are tangents to the circle with centre O.
• ∠P = 90°, meaning △APB is a right-angled triangle.
• AB `3sqrt2` cm is the hypotenuse of the right triangle △APB.

Since O is the centre and the radius is perpendicular to the tangents, OP is the radius of the circle.

Step 1: Apply Pythagoras Theorem 

Since AB is the hypotenuse of the right-angled triangle △APB. 

AB² = AP² + PB²

Since the tangents from an external point are equal, AP = PB = r (radius of the circle)

`(3sqrt2)^2 = r^2 + r^2`

18 = 2r²

r² = 9

r = 3 cm

Step 2: Find the Diameter

Diameter = 2r = 2 × 3 = 6 cm