Advertisements
Advertisements
प्रश्न
In the figure given below, a folding table is shown.
The legs of the table are represented by line segments AB and CD intersecting at O. Join AC and BD. Considering table top is a parallel to the ground and OB = x, OD = x + 3, OC = 3x + 19 and OA = 3x + 4, answer the following questions.
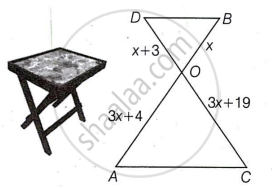
- Prove that ΔOAC is similar to ΔOBD. [1]
- Prove that `(OA)/(AC) = (OB)/(BD)`. [1]
-
- Observe the figure and find the value of x. Hence, find the length of OC. [2]
OR - Observe the figure and find `(BD)/(AC)`. [2]
- Observe the figure and find the value of x. Hence, find the length of OC. [2]
उत्तर
Given OB = x, OD = x + 3, OC = 3x + 19 and OA = 3x + 4
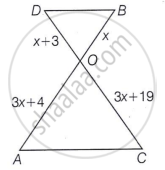
and AC || BD
(i) ΔOAC ∼ ΔOBD
In ΔOAC and ΔOBD
∠DOB = ∠COA ..[Vertically opposite angles]
As, AC is parallel to BD, AB and DC are transversal
∠BAC = ∠ABD
and ∠CDB = ∠DCA ...[∵ Alternate interior angles]
ΔOAC ∼ ΔOBD ...[by AA similarity criteria]
(ii) `(OA)/(AC) = (OB)/(BD)`
From part (i) we know that
ΔOAC ∼ ΔOBD
Corresponding sides of ΔOAC and ΔOBD must be proportional
`(OA)/(OB) = (AC)/(BD)`
∴ `(OA)/(AC) = (OB)/(BD)`
(iii)
(a) From part (i)
ΔOAC ∼ ΔOBD
⇒ `(OA)/(OB) = (OC)/(OD)`
⇒ `(3x + 4)/x = (3x + 19)/(x + 3)` ...[Given OA = 3x + 4, OB = x, OC = 3x + 19, OD = x + 3]
⇒ (3x + 4)(x + 3) = (3x + 19)x
⇒ 3x2 + 9x + 4x + 12 = 3x2 + 19x
⇒ 13x + 12 = 19x
⇒ 19x − 13x = 12
⇒ 6x = 12
⇒ x = 2
Given, OC = 3x + 19
= 3 × (2) + 19
= 6 + 19
= 25
∴ OC = 25
OR
(b) From part (ii), we have
`(OA)/(AC) = (OB)/(BD)`
`(BD)/(AC) = (OB)/(OA)`
`(BD)/(AC) = x/(3x + 4)` ...[Given, OB = x and OA = 3x + 4]
On substituting x = 2, we get
`(BD)/(AC) = 2/(3 xx 2 + 4)`
∴`(BD)/(AC) = 2/10`
∴`(BD)/(AC) = 1/5`
