Question

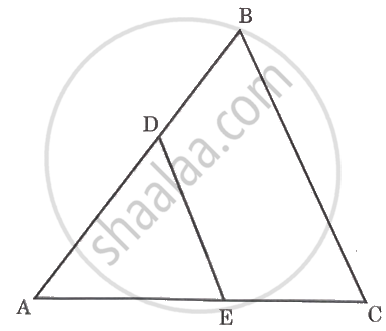
In the following figure, DE || BC, then:

1. If DE = 4 cm, BC = 8 cm, A(ΔADE) = 25 cm², find A(ΔABC).
2. If DE : BC = 3 : 5, then find A(ΔADE) : A(`square`DBCE).

Answer 1

In ΔABC and ΔADE

∠ABC ≅ ∠ADE  ...(DE || BC, Corresponding angles)

∠BAC ≅ ∠DAE  ...(Common angles)

∴ ΔABC ∼ ΔADE  ...(AA Test of similarity)

(i) Given: DE = 4 cm, BC = 8 cm, A(△ADE) = 25 cm²

∴ By theorem of areas of similar triangles

`(A(ΔABC))/(A(ΔADE)) = (BC^2)/(DE^2)`

∴ `(A(ΔABC))/25 = 8^2/4^2`

∴ A(ΔABC) = `(25 xx 64)/16`

∴ A(ΔABC) = 100 cm²

(ii) Given: `(DE)/(BC) = 3/5`

∴ By theorem of areas of similar triangles

`(A(ΔADE))/(A(ΔABC)) = (DE^2)/(BC^2)`

∴ `(A(ΔADE))/(A(ΔABC)) = 3^2/5^2`

∴ `(A(ΔADE))/(A(ΔABC)) = 9/25`

Let A(ΔADE) = 9x then A(ΔABC) = 25x.

Since A(`square`DBCE) = A(ΔABC) − A(ΔADE)

∴ A(`square`DBCE) = 25x − 9x

∴ A(`square`DBCE) = 16x

Now, `(A(ΔADE))/(A(squareDBCE)) = (9x)/(16x)`

∴ `(A(ΔADE))/(A(squareDBCE)) = 9/16`

∴ A(△ADE) : A(`square`DBCE) = 9 : 16