Advertisements
Advertisements
प्रश्न
In the given figure, `angle`ABC = `angle`ACB and `(BC)/(BE) = (BD)/(AC)`.
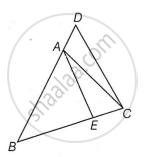
Show that `triangle`ABE ∼ `triangle`DBC and AE || DC.
योग
उत्तर
Given, `angle`ABC = `angle`ACB
∴ AB = AC ...[∵ sides opposite to equal angles of a triangle are equal]
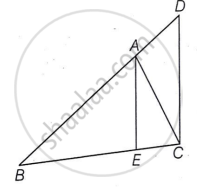
In `triangle`ABE and `triangle`DBC,
`angle`ABE = `angle`DCB ...[Common]
`(BC)/(BE) = (BD)/(AC)` ...[Given]
`(BC)/(BE) = (BD)/(AB)` ...[∵ AB = AC]
So, `triangle`ABC ∼ `triangle`DBE
Now, `(BC)/(BE) = (BD)/(AB)`
Then, by the converse of the Basic Proportionality Theorem, if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
∴ AE || AD
shaalaa.com
क्या इस प्रश्न या उत्तर में कोई त्रुटि है?
