Question

In the given figure, if ∠a ≅ ∠b then prove that line l || line m.

Answer 1

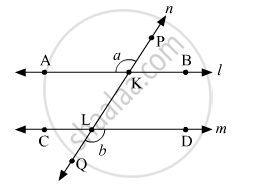
Let us mark the points A and B on line l, C and D on line m and P and Q on line n.

Suppose the line n intersect line l at K and line m at L.

Since PQ is a straight line and ray KA stands on it, then

m∠AKP + m∠AKL = 180^∘    ...(Angles in a linear pair)

⇒ m∠a + m∠AKL = 180^∘

⇒ m∠a = 180^∘ − m∠AKL    ....(1)

Since PQ is a straight line and ray LD stands on it, then

m∠DLQ + m∠DLK = 180^∘    ...(Angles in a linear pair)

⇒ m∠b + m∠DLK = 180^∘

⇒ m∠b = 180^∘ − m∠DLK    ....(2)

Since, ∠a ≅ ∠b, then m∠a = m∠b 

∴ from (1) and (2), we get

180^∘ − m∠AKL = 180^∘ − m∠DLK

⇒ m∠AKL = m∠DLK

⇒ ∠AKL ≅ ∠DLK

It is known that, if a pair of alternate interior angles formed by a transversal of two lines is congruent, then the two lines are parallel.

∴ AB || CD or line l || line m.