Question

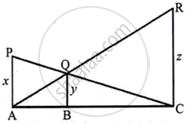
In the given figure PA, QB and RC are each perpendicular to AC. If AP = x, BQ = y and CR = z, then prove that `1/x + 1/z = 1/y`

Answer 1

In ΔCAP and CBQ

∠CAP = ∠CBQ = 90°

∠PCA = ∠QCB   (common angle)

So, ΔCAP ∼ ΔCBQ     ...(By AA similarly Rule)

Hence, `(BQ)/(AP) = (BC)/(AC) ⇒ y/x = (BC)/(AC)`   ...(i)

Now, in ΔACR and ΔABQ

∠ACR = ∠ABQ = 90°

∠QAB = ∠RAC      ...(common angle)

So, ΔACR ∼ ΔABQ  (By AA similarity Rule)

Hence, `(BQ)/(CR) = (AB)/(AC) ⇒ y/z = (AB)/(AC)`   ...(ii)

On adding eq. (i) and (ii), we get

`y/x + y/z = (BC)/(AC) + (AB)/(AC)`

`y(1/x + 1/z) = (BC + AB)/(AC)`

`y(1/x + 1/z) = (AC)/(AC)`

⇒ `y(1/x + 1/z) = 1`

`1/x + 1/z = 1/y`

Hence Proved