Question

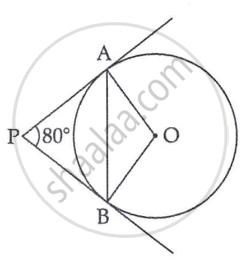
In the given figure, tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80°. ∠ABO is equal to ______.

विकल्प

• 40°

• 80°

• 100°

• 50°

Answer 1

In the given figure, tangents PA and PB from a point P to a circle with centre O         are inclined to each other at an angle of 80°. ∠ABO is equal to 40°.

Explanation:

In ΔOAB , we have

OA = OB   ...(radii of same circle)

∴ ∠ABO = ∠BAO   ...(Angles opposite to equal sides are equal)

As PA and PB are tangents from a point P to a circle with centre O.

So, ∠OAP = 90°

Similarly, ∠OBP = 90°   ...(∵ tangents drawn from an external point to a circle are perpendicular to the circle)

Now, in quadrilateral PAOB,

∠P + ∠A + ∠O + ∠B = 360°

⇒ ∠80° + 90° + ∠O + 90° = 360°

⇒ ∠O = 360° − (90° + 90° + 80°)

∠O = 100°

Again, in ΔOAB,

∠O + ∠ABO + ∠BAO = 180°   ...(Angle sum property)

100° + ∠ABO + ∠BAO = 180°   ...(∵ ∠ABO = ∠BAO)

⇒ 2 ∠ABO = 180° − 100° = 80°

⇒ ∠ABO = 40°