Advertisements
Advertisements
प्रश्न
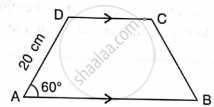
In trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠ A = 60°. Find: length of AB
उत्तर
First, draw two perpendiculars to AB from point D and C respectively. Since AB || CD therefore PMCD will be a rectangle.
Consider the figure,
From right triangle ADP we have
cos 60° = `"AP"/"AD"`
`(1)/(2) = "AP"/(20)`
AP = 10
Similarly from the right triangle BMC we have BM = 10 cm.
Now from the rectangle PMCD we have CD = PM = 20 cm.
Therefore,
AB = AP + PM + MB = 10 + 20 + 10 = 40 cm.
APPEARS IN
संबंधित प्रश्न
Find angle 'A' if :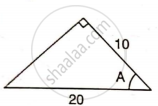
Find AD, if:
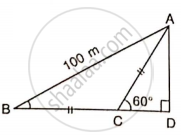
Find the lengths of diagonals AC and BD. Given AB = 60 cm and ∠ BAD = 60°.

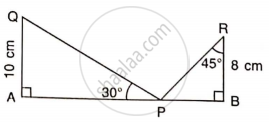
Find AB.
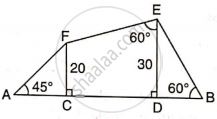
Use the information given to find the length of AB.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
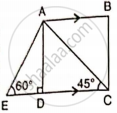
Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AE.
Find: BC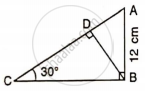
In right-angled triangle ABC; ∠ B = 90°. Find the magnitude of angle A, if: AB is √3 times of BC.
If tan x° = `(5)/(12)`,
tan y° = `(3)/(4)` and AB = 48 m; find the length of CD.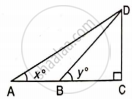
The perimeter of a rhombus is 96 cm and obtuse angle of it is 120°. Find the lengths of its diagonals.
