Question

It takes 24 hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for 8 hours and the pipe of the smaller diameter is used for 18 hours. Only half of the pool is filled. How long would each pipe take to fill the swimming pool

Answer 1

Let the time taken by the larger diameter pipe be “x” hours and the time taken by the smaller diameter pipe be “y” hours.

By the given first condition

`1/x + 1/y = 1/24` → (1)

Also

In 8 hours the large pipe fill `8/x`

In 18 hours the smaller pipe fill `18/y`

By the given second condition (`1/2` of the tank)

`8/x + 18/y = 1/2` → (2)

Solve (1) and (2) we get

Let `1/x` = a, `1/y` = b

a + b = `1/24`

Multiply by 24

24a + 24b = 1

24a + 24b – 1 = 0 → (3)

8a + 18b = `1/2`

Multiply by 2

16a + 36b = 1

16a + 36b – 1 = 0 → (4)

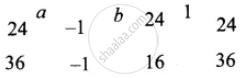
`"a"/(-24 - (-36)) = "b"/(-16 - (-24)) = 1/(864 - 384)`

`"a"/(-24 + 36) = "b"/(-16 + 24) = 1/480`

`"a"/12 = "b"/8 = 1/480`

`"a"/12 = 1/480`

480a = 12 ⇒ a = `12/480 = 1/40`

`"b"/8 = 1/480`

b = `8/480 = 1/60`

But `1/x` = a ⇒ `1/x = 1/40`

x = 40

`1/"y"` = b ⇒ `1/y = 1/60`

y = 60

To fill the remaining half of the pool.

Time taken by larger pipe = `1/2` × 40 = 20 hours

Time taken by smaller pipe = `1/2` × 60 = 30 hours