Question

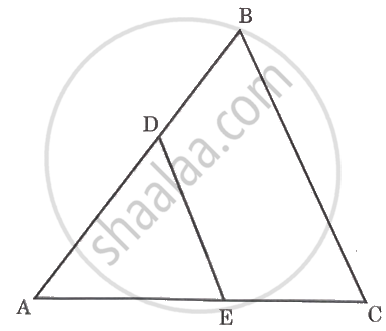
खालील आकृतीमध्ये DE || बाजू BC

1. जर DE = 4 सेमी, BC = 8 सेमी, A(ΔADE) = 25 सेमी², तर A(ΔABC) काढा. 
2. जर DE : BC = 3 : 5, तर A(ΔADE) : A(`square`DBCE) काढा.

Answer 1

ΔABC आणि ΔADE मध्ये

∠ABC ≅ ∠ADE ...(DE || BC, संगत कोन)

∠BAC ≅ ∠DAE ...(सामाईक कोन)

∴ ΔABC ∼ ΔADE ...(कोको कसोटी)

(i) पक्ष: DE = 4 सेमी, BC = 8 सेमी, A(△ADE) = 25 सेमी²

∴ समरूप त्रिकोणांच्या क्षेत्रफळांच्या प्रमेयानुसार

`(A(ΔABC))/(A(ΔADE)) = (BC^2)/(DE^2)`

∴ `(A(ΔABC))/25 = 8^2/4^2`

∴ A(ΔABC) = `(25 xx 64)/16`

∴ A(ΔABC) = 100 सेमी²

(ii) पक्ष: `(DE)/(BC) = 3/5`

∴ समरूप त्रिकोणांच्या क्षेत्रफळांच्या प्रमेयानुसार

`(A(ΔADE))/(A(ΔABC)) = (DE^2)/(BC^2)`

∴ `(A(ΔADE))/(A(ΔABC)) = 3^2/5^2`

∴ `(A(ΔADE))/(A(ΔABC)) = 9/25`

समजा A(ΔADE) = 9x तर A(ΔABC) = 25x.

कारण A(`square`DBCE) = A(ΔABC) − A(ΔADE)

∴ A(`square`DBCE) = 25x − 9x

∴ A(`square`DBCE) = 16x

आता, `(A(ΔADE))/(A(squareDBCE)) = (9x)/(16x)`

∴ `(A(ΔADE))/(A(squareDBCE)) = 9/16`

∴ A(△ADE) : A(`square`DBCE) = 9 : 16