Question

Lenses are constructed by a material of refractive index 1.50. The magnitude of the radii of curvature are 20 cm and 30 cm. Find the focal lengths of the possible lenses with the above specifications.

Answer 1

Given,
Refractive index of the material, (μ) = 1.50
Magnitudes of the radius of curvature:
R₁ = 20 cm and R₂ = 30 cm

From the given data we can make four possible lenses, using the lens maker formula.
\[\frac{1}{f} = (\mu - 1)\left( \frac{1}{R_1} - \frac{1}{R_2} \right)\]

Four possible lenses:
(a) 1^st lens is double convex, in which R₁ = +20 cm and R₂ = −30 cm
\[= 0 . 5\left[ \frac{1}{20} - \frac{1}{\left( - 30 \right)} \right] = \frac{0 . 5 \times 5}{60}\]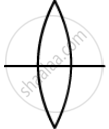

(b) 2^nd lens is double concave, in which R₁ = −20 cm and R₂ = +30 cm
\[= 0 . 5\left[ \frac{- 1}{20} - \frac{1}{30} \right]\]
f = −24 cm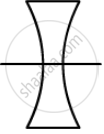

(c) 3^rd lens is concave concave in which R₁ = −20 cm and R₂ = −30 cm
\[= 0 . 5\left[ \frac{- 1}{20} - \frac{1}{\left( - 30 \right)} \right]\]
f = −120 cm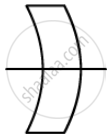

(d) 4^th lens is concave convex, in which R₁ = +20 cm and R₂ = +30 cm
\[= 0 . 5\left[ \frac{1}{20} - \frac{1}{30} \right]\] 
 ​f = +120 cm