Advertisements
Advertisements
प्रश्न
Let A, B be the centres of two circles of equal radii; draw them so that each one of them passes through the centre of the other. Let them intersect at C and D. Examine whether `overline("AB")` and `overline"CD"` are at right angles.
उत्तर
Let us draw two circles of same radius which are passing through the centres of the other circle.
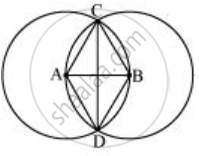
Here, point A and B are the centres of these circles and these circles are intersecting each other at point C and D.
In quadrilateral ADBC,
AD = AC (Radius of circle centered at A)
BC = BD (Radius of circle centered at B)
As radius of both circles are equal, therefore, AD = AC = BC = BD
Hence, `square"ADBC"` is a rhombus and in a rhombus, the diagonals bisect each other at 90°. Hence, `overline("AB")` and `overline"CD"` are at right angles.
APPEARS IN
संबंधित प्रश्न
Draw circle for the following measurements of radius(r)/diameters(d)
r = 4 cm
Draw circle for the following measurements of radius(r)/diameters(d)
d = 12 cm
Draw circle for the following measurements of radius(r)/diameters(d)
r = 3.5 cm
Draw circle for the following measurements of radius(r)/diameters(d)
r = 6.5 cm
Draw circle for the following measurements of radius(r)/diameters(d)
d = 6 cm
With a given centre and a given radius, only one circle can be drawn.
Draw a circle of radius 6 cm using ruler and compasses. Draw one of its diameters. Draw the perpendicular bisector of this diameter. Does this perpendicular bisector contain another diameter of the circle?
With the same centre O, draw two circles of radii 4 cm and 2.5 cm.
Draw a circle and any two of its diameters. If you join the ends of these diameters, what is the figure obtained? What figure is obtained if the diameters are perpendicular to each other? How do you check your answer?
