Question

Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.

विकल्प

• 1

• `1/2`

• `1/sqrt(2)`

• `2sqrt(2)`

Answer 1

Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to `underlinebb(1/2)`.

Explanation:

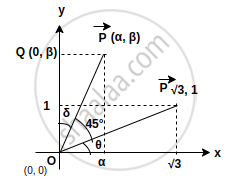
Let `vecP = sqrt(3)hati + hatj` 

⇒ tanθ = `(1/sqrt(3))`

⇒ θ = 30°

`vecp^' = αhati + βhatj`

θ + 45° + δ = 90°

⇒ δ = 45° – 30°

δ = 15°

Now, Area of ΔOP'Q

= `1/2(OP^' cos15^circ) xx (OP^' sin15^circ)`

= `1/4(2sin15^circ cos15^circ)(OP^')^2`

= `1/4(sin30^circ)(OP^')^2`

= `1/4(1/2)(sqrt((3)^2 + 1^2)) = 1/2`  ...[∵ OP = OP']