Question

Let P be a plane Ix + my + nz = 0 containing the line, `(1 - x)/1 = ("y" + 4)/2 = ("z" + 2)/3`. If plane P divides the line segment AB joining points A(–3, –6, 1) and B(2, 4, –3) in ratio k:1 then the value of k is equal to ______.

विकल्प

• 1.5

• 2

• 4

• 3

Answer 1

Let P be a plane Ix + my + nz = 0 containing the line, `(1 - x)/1 = ("y" + 4)/2 = ("z" + 2)/3`. If plane P divides the line segment AB joining points A(–3, –6, 1) and B(2, 4, –3) in ratio k:1 then the value of k is equal to 2.

Explanation:

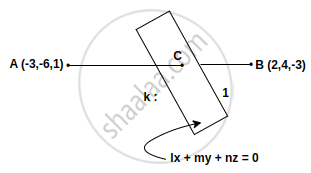
Given; A(–3, –6, 1), B(2, 4, –3)

Plane P divide the line segment AB in the ratio k:1

`C((2"k" - 3)/("k" + 1), (4"k" - 6)/("k" + 1), (-3"k" + 1)/("k" + 1))`

Equation of line `(1 - x)/1 = ("y" + 4)/2 = ("z" + 2)/3` satisfied to the plane then, lx + my + nz = 0

⇒ l(–1) + m(2) + n(3) = 0

⇒ –1 + 2m + 3n = 0  ...(ii)

Since, lx +  my + nz = 0 also satisfy point (1, –4, –2)

Then, l – 4m – 2n = 0  ...(iii)

Now using (ii) and (iii)

n = 2m

l = 8m

`"l"/8 = "m"/1 = "n"/2`

l:m:n = 8:1:2

Equation of plane will be 8x + y + 2z = 0

Point C will satisfy Bx + y + 2z = 0, then `8((2"k" - 3)/("k" + 1)) + ((4"k" - 6)/("k" + 1)) + 2((-3"k" + 1)/("k" + 1))`

⇒ 16k – 24 + 4k – 6 – 6k + 2 = 0

⇒ k = 2